题目内容
13.已知2a-1的平方根是3,3a+b-1的算术平方根是4,c是$\sqrt{15}$的整数部分,d的立方根是$\root{3}{3}$,x、y都是实数,且满足y=$\sqrt{3-x}$+$\sqrt{x-3}$+13,求$\sqrt{ab+cd+y+x+1}$的平方根.分析 根据平方根,算术平方根,估算无理数的大小,二次根式的性质分别求出a、b、c、d、x、y的值,代入求出即可.
解答 解:∵2a-1的平方根是3,3a+b-1的算术平方根是4,c是$\sqrt{15}$的整数部分,d的立方根是$\root{3}{3}$,x、y都是实数,且满足y=$\sqrt{3-x}$+$\sqrt{x-3}$+13,
∴2a-1=9,3a+b-1=16,c=3,b=3,x=3,y=13,
∴a=5,b=2,
∴ab+cd+y+x+1=10+9+3+13+1=26,
∴$\sqrt{ab+cd+y+x+1}$的平方根是±$\sqrt{26}$.
点评 本题考查了二次根式有意义的条件,平方根、算术平方根,估算无理数的值等知识点,能根据知识点求出2a-1=9、3a+b-1=16、c=3、b=3、x=3、y=13是解此题的关键.

练习册系列答案
相关题目
3.计算(-a)3•(a2)3的结果正确的是( )
| A. | a11 | B. | -a11 | C. | -a9 | D. | a8 |
4.某校女子排球队队员的年龄分布如下表
则该校女子排球队队员的年龄中位数是13岁.
| 年龄(岁) | 13 | 14 | 15 |
| 人数(人) | 8 | 4 | 3 |
8.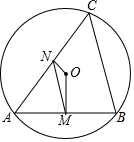 如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
 如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{2}$$\sqrt{3}$ | D. | $\frac{1}{2}\sqrt{2}$ |
2.QQ运动记录的小莉爸爸2017年2月份7天步行的步数(单位:万步)如下表:
(1)制作适当的统计图表示小莉爸爸这7天步行的步数的变化趋势;
(2)求小莉爸爸这7天中每天步行的平均步数;
(3)估计小莉爸爸2月份步行的总步数.
| 日期 | 2月6日 | 2月7日 | 2月8日 | 2月9日 | 2月10日 | 2月11日 | 2月12日 |
| 步数 | 2.1 | 1.7 | 1.8 | 1.9 | 2.0 | 1.8 | 2.0 |
(2)求小莉爸爸这7天中每天步行的平均步数;
(3)估计小莉爸爸2月份步行的总步数.
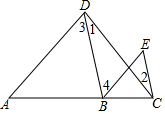 按图填空,并注明理由
按图填空,并注明理由