题目内容
有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形,且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了右图,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )

A. B.
B. C.
C. D.
D.
B.
【解析】
试题分析:设直角三角形的是三条边分别是a,b,c,根据勾股定理,得 ,
,
即:正方形A的面积+正方形B的面积=正方形C的面积=1;
所有正方形的面积之和为2=(1+1)×1;
正方形E的面积+正方形F的面积=正方形A的面积,
正方形M的面积+正方形N的面积=正方形B的面积,
正方形E的面积+正方形F的面积+正方形M的面积+正方形N的面积,
=正方形A的面积+正方形B的面积=正方形C的面积=1,
所有正方形的面积之和为3=(2+1)×1,
…
推而广之,“生长”了k次后形成的图形中所有的正方形的面积和是(k+1)×1=k+1,
故选B.

考点:1.勾股定理;2.规律型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (单位:米)与车速
(单位:米)与车速 (单位:米/秒)之间有如下关系:
(单位:米/秒)之间有如下关系: ,其中
,其中 为司机的反应时间(单位:秒),
为司机的反应时间(单位:秒), 为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数
为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数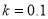 ,并测得志愿者在未饮酒时的反应时间
,并测得志愿者在未饮酒时的反应时间 秒.
秒.





 的对称轴是( )
的对称轴是( )