Question

（本题10分）司机在驾驶汽车时，发现紧急情况到踩下刹车需要一段时间，这段时间叫反应时间，之后还会继续行驶一段距离．我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”（如图）．

已知汽车的刹车距离（单位：米）与车速（单位：米/秒）之间有如下关系：，其中为司机的反应时间（单位：秒），为制动系数．某机构为测试司机饮酒后刹车距离的变化，对某种型号的汽车进行了“醉汉”驾车测试，已知该型号汽车的制动系数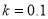，并测得志愿者在未饮酒时的反应时间秒．

（1）若志愿者未饮酒，且车速为10米/秒，则该汽车的刹车距离为 米 ；

（2）当志愿者在喝下一瓶啤酒半小时后，以15米/秒的速度驾车行驶，测得刹车距离为52.5米，此时该志愿者的反应时间是 秒．

（3）假如该志愿者当初是以10米/秒的车速行驶，则刹车距离将比未饮酒时增加多少？

 

Answer 1

（1）15米；（2）2秒；（3）增加15米．

【解析】

试题分析：（1）把k=0.1，t=0.5，v=10代入即可得到刹车距离；

（2）把k=0.1，v=15，s=52.5代入所给函数可得t的值；

（3）把v=10，t=0.5，k=0.1代入s=tv+kv2中得出s的值即可．

试题解析：（1）把k=0.1．t=0.5，v=10代入s=tv+kv2中得：s=0.5×10+0.1×102=15；

故答案为：15；

（2）把v=15，s=52.5，k=0.1代入s=tv+kv2中得：52．5=15t+0.1×152，解得：t=2，

（3）把v=10，t=2，k=0.1代入s=tv+kv2中得：s=10×2+0.1×102=30，

把v=10，t=0.5，k=0.1代入s=tv+kv2中得：s=10×0.5+0.1×102=15，

30﹣15=15，

故答案为：2；30；15．

考点：一元一次方程的应用．