��Ŀ����
7����������Ҫ������������1���벹ȫ������ʽ-2x2-4x��0�Ľ⼯�Ĺ���
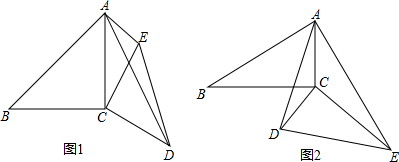
�ٹ��캯��������ͼ���ݲ���ʽ����������κ���y=-2x2-4x���������������ϵ�У���ͼ1���������κ���y=-2x2-4x��ͼ��ֻ����ͼ�ɣ�
����ý�㣬��ʾ���裻��y=0ʱ����÷���-2x2-4x=0�Ľ�Ϊx1=0��x2=-2�����þ���߱�ʾ������y=-2x2-4xͼ����y��0�IJ��֣�
�۽���ͼ��д���⼯��������ʾͼ�ɵò���ʽ-2x2-4x��0�Ľ⼯Ϊ-2��x��0��
��2�����ã�1������ʽ�⼯�IJ��裬��ʽx2-2x+1��4�Ľ⼯
�ٹ��캯��������ͼ�� ����ý�㣬��ʾ���� �۽���ͼ��д���⼯
��3����������������ʽ�⼯�Ĺ��̣�����һԪ���η��̵������ʽ��ֱ��д������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��
���� ��1��������������x��Ľ������꣬�����ߵĿ��ڷ����Լ������ߵĶԳ�������ͼ����ͼ��д������ʽ-2x2-4x��0�Ľ⼯��
��2���ο���1���Ľ�����̽��м��㣻
��3���ο���1���Ľ�����̽��м��㣮������Ҫ�������ۣ�����0����=0������0���������
��� �⣺��1��y=-2x2-4x=-2x��x+2���������������x�ύ�������ֱ��ǣ�0��0������-2��0�����������߿��ڷ������£����������ͼ����ͼ��1����ʾ��

����ͼʾ֪������ʽ-2x2-4x��0�Ľ⼯Ϊ-2��x��0��
�ʴ��ǣ�x1=0��x2=-2��-2��x��0��
��2���ٹ��캯��y=x2-2x+1������ͼ����ͼ��2����ʾ��
�ڵ�y=4ʱ������x2-2x+1=4�Ľ�Ϊx1=-1��x2=3��
����ͼ��2��֪������ʽx2-2x+1��4�Ľ⼯��-1��x��3��
��3���ٵ�b2-4ac��0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��x��$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$��x��$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$��
��b2-4ac=0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��x��-$\frac{b}{2a}$��
��b2-4ac��0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��ȫ��ʵ����
���� ���⿼���˶��κ����벻��ʽ���飩�����ν������ѧ�е���Ҫ˼��֮һ������������������ˣ�ͬѧ��Ҫ�������ӣ�

��2���ⷽ�̣�1-$\frac{1}{x-1}$=$\frac{2x}{1-x}$��
| A�� | a=2012 | B�� | a��2012 | C�� | a��2012 | D�� | ��ȷ�� |
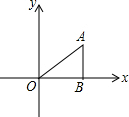 ��ͼ���ڡ�ABO�У�AB��OB��OB=$\sqrt{3}$��AB=1������ABO��O����ת90���õ���A1B1O�����A1������Ϊ��������
��ͼ���ڡ�ABO�У�AB��OB��OB=$\sqrt{3}$��AB=1������ABO��O����ת90���õ���A1B1O�����A1������Ϊ��������| A�� | ��-1��$\sqrt{3}$�� | B�� | ��-1��$\sqrt{3}$����1��-$\sqrt{3}$�� | C�� | ��-1��-$\sqrt{3}$�� | D�� | ��-1��-$\sqrt{3}$����-$\sqrt{3}$��-1�� |
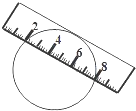 ��ͼ��һ��Ϊ2cm�Ŀ̶ȳ���Բ���ƶ������̶ȳߵ�һ����Բ����ʱ����һ����Բ�������㴦�Ķ���ǡ��Ϊ��2���͡�8������λ��cm�������Բ�İ뾶Ϊ$\frac{13}{4}$cm��
��ͼ��һ��Ϊ2cm�Ŀ̶ȳ���Բ���ƶ������̶ȳߵ�һ����Բ����ʱ����һ����Բ�������㴦�Ķ���ǡ��Ϊ��2���͡�8������λ��cm�������Բ�İ뾶Ϊ$\frac{13}{4}$cm��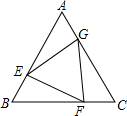 ��ͼ����֪����ABC�ı߳�Ϊ2��E��F��G�ֱ���AB��BC��CA�ϵĵ㣬��AE=BF=CG�����EFG�����Ϊy��AE�ij�Ϊx����y����x�ĺ���ͼ������ǣ�������
��ͼ����֪����ABC�ı߳�Ϊ2��E��F��G�ֱ���AB��BC��CA�ϵĵ㣬��AE=BF=CG�����EFG�����Ϊy��AE�ij�Ϊx����y����x�ĺ���ͼ������ǣ�������