题目内容
2.已知A点的坐标为(-1,3),将A点绕坐标原点顺时针90°,则点A的对应点的坐标为(3,1).分析 过A作AC⊥y轴于C,过A'作A'D⊥x轴于D,根据旋转求出∠A=∠A'OD,证△ACO≌△ODA',推出A'D=OC=1,OD=CA=3,即可根据题意作出A点绕坐标原点顺时针90°后的点,然后写出坐标.
解答 解:过A作AC⊥y轴于C,过A'作A'D⊥y轴于D,
∵∠AOA'=90°,∠ACO=90°,
∴∠AOC+∠A'OD=90°,∠A+∠AOC=90°,
∴∠A=∠A'OD,
在△AC0和△ODA'中,
$\left\{\begin{array}{l}{∠OCA=∠ODA'}\\{∠CAO=∠A'OD}\\{OA=OA'}\end{array}\right.$,
∴△AC0≌△ODA'(AAS),
∴A'D=OC=1,OD=CA=3,
∴A'的坐标是(3,1).
故答案为:(3,1).
点评 本题主要考查对坐标与图形变换-旋转,全等三角形的性质和判定等知识点的理解和掌握,能正确画出图形并求出△AC0≌△ODA'是解此题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
11.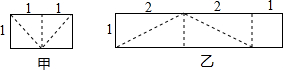 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )| A. | 甲、乙都可以 | B. | 甲、乙都不可以 | C. | 甲不可以、乙可以 | D. | 甲可以、乙不可以 |
12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
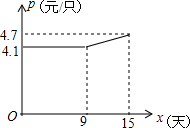 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$