题目内容
19.(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.
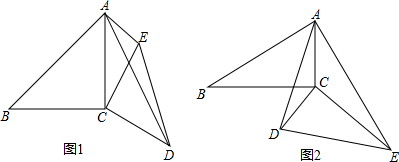
分析 (1)连接BE,证明△ACD≌△BCE,得到AD=BE,在Rt△BAE中,AB=6$\sqrt{2}$,AE=3,求出BE,得到答案;
(2)连接BE,证明△ACD∽△BCE,得到$\frac{AD}{BE}$=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,求出BE的长,得到AD的长.
解答 解:(1)如图1,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠BCE=∠ACD}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE,
∵AC=BC=6,
∴AB=6$\sqrt{2}$,
∵∠BAC=∠CAE=45°,
∴∠BAE=90°,
在Rt△BAE中,AB=6$\sqrt{2}$,AE=3,
∴BE=9,
∴AD=9;
(2)如图2,连接BE,
在Rt△ACB中,∠ABC=∠CED=30°,
tan30°=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD,
∴△ACD∽△BCE,
∴$\frac{AD}{BE}$=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∵∠BAC=60°,∠CAE=30°,
∴∠BAE=90°,又AB=6,AE=8,
∴BE=10,
∴AD=$\frac{10}{3}\sqrt{3}$.
点评 本题考查的是相似三角形的判定和性质、全等三角形的判定和性质,掌握性质定理和判定定理是解题的关键,正确作出辅助线是重点.

练习册系列答案
相关题目
9.如图,下列四个几何体中,它们各自的三视图(主视图.左视图.俯视图)完全相同的几何体是( )


| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
4.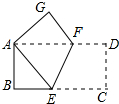 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )| A. | AF=AE | B. | △ABE≌△AGF | C. | EF=2$\sqrt{5}$ | D. | AF=EF |
11.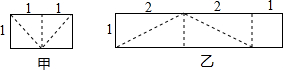 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )| A. | 甲、乙都可以 | B. | 甲、乙都不可以 | C. | 甲不可以、乙可以 | D. | 甲可以、乙不可以 |
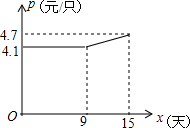 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.