题目内容
16．已知$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$且-1＜x-y＜0，则k的取值范围为（ ）| A． | -1＜k＜-$\frac{1}{2}$ | B． | $\frac{1}{2}$＜k＜1 | C． | 0＜k＜1 | D． | 0＜k＜$\frac{1}{2}$ |
分析 先根据方程组将两式相减，得到x-y=1-2k，再代入-1＜x-y＜0，得到关于k的不等式组，进而得出k的取值范围．
解答 解：∵$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$
∴（2x+y）-（x+2y）=（2k+1）-4k，
∴x-y=1-2k，
又∵-1＜x-y＜0，
∴-1＜1-2k＜0，
解得$\frac{1}{2}$＜k＜1．
故选：B．
点评 本题主要考查了解一元一次不等式组以及解二元一次方程组，解决问题的关键是根据方程组求得x-y=1-2k，运用整体思想进行代入计算．
练习册系列答案
相关题目
如图，一个正方形被分成了九个大小相等的小方形，其中两个小正方形涂了颜色，涂色后的大正方形仍然是一个轴对称图形．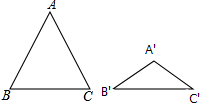
如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为25：9．
5．下列说法正确的是（ ）
| A． | 带正号的数是正数 | B． | 带负号的数是负数 | ||
| C． | 负数一定带有负号 | D． | 正数一定带有正号 |