题目内容
14.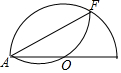 将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )| A. | 5 | B. | 5$\sqrt{2}$ | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
分析 首先过点O作OB⊥AF交半圆O于C,垂足为B,由垂径定理,即可得AB=BF=$\frac{1}{2}$AF,又由折叠的性质得:OB=BC=$\frac{1}{2}$OC,然后在Rt△ABO中,求得AB的长,即可得AF的长.
解答  解:过点O作OB⊥AF交半圆O于C,垂足为B,
解:过点O作OB⊥AF交半圆O于C,垂足为B,
∵OB⊥AF,
∴AB=BF=$\frac{1}{2}$AF,
由折叠的性质得:OB=BC=$\frac{1}{2}$OC,
∵半圆O的半径为5cm,
∴OB=$\frac{5}{2}$,
在Rt△ABO中,AB=$\sqrt{A{O}^{2}-B{O}^{2}}$=$\frac{5\sqrt{3}}{2}$,
∴AF=5$\sqrt{3}$.
故选C.
点评 此题考查了垂径定理与折叠的性质,以及勾股定理的应用.此题难度不大,解题的关键是注意辅助线的作法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.△ABC中,AB=13,BC=10,BC边上中线AP=12,则AB,AC关系为( )
| A. | AB>AC | B. | AB=AC | C. | AB<AC | D. | 无法确定 |
4.在解方程$\frac{x-1}{2}$=1-$\frac{2x+3}{3}$时,去分母正确的是( )
| A. | 3(x-1)=1-2(2+3x) | B. | 3(x-1)=1+2(2x+3) | C. | 3(x-1)=6-2(2x+3) | D. | 3(x-1)=6+2(2x+3) |
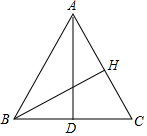 如图,AD是△ABC的中线,AD=12,AB=13,BC=10,
如图,AD是△ABC的中线,AD=12,AB=13,BC=10,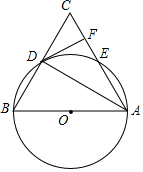 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.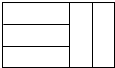 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.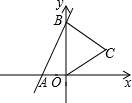 如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).
如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).