题目内容
4.对有理数a、b、c、d定义新运算“$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$”,规定$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,请你根据新定义解答下列问题:(1)计算$|\begin{array}{l}{2x-3y}&{4x}\\{x-5}&{2x+3y}\end{array}|$;
(2)当x=$\frac{1}{5}$,y=-$\frac{2}{3}$时,求上式的值.
分析 (1)根据题目中的新定义可以化简所求的式子;
(2)将x、y的值代入(1)中化简后的式子即可解答本题.
解答 解:(1)由题意可得,
$|\begin{array}{l}{2x-3y}&{4x}\\{x-5}&{2x+3y}\end{array}|$
=(2x-3y)(2x+3y)-4x(x-5)
=4x2-9y2-4x2+20x
=-9y2+20x;
(2)当x=$\frac{1}{5}$,y=-$\frac{2}{3}$时,
-9y2+20x=-9×$(-\frac{2}{3})^{2}+20×\frac{1}{5}$=-9×$\frac{4}{9}$+4=-4+4=0.
点评 本题考查整式的混合运算、新定义,解题的关键是明确整式的混合运算的计算方法和利用新定义解答问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.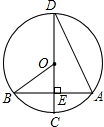 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
14.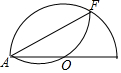 将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
 将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )| A. | 5 | B. | 5$\sqrt{2}$ | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
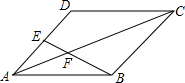 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.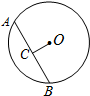 如图,在⊙O中,点C是AB的中点,AB=4cm,OC=1cm,则OB的长是$\sqrt{5}$cm.
如图,在⊙O中,点C是AB的中点,AB=4cm,OC=1cm,则OB的长是$\sqrt{5}$cm.