题目内容
11.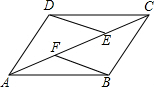 已知如图在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:∠AED=∠CFB.
已知如图在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:∠AED=∠CFB.
分析 由四边形ABCD是平行四边形,得到AD=BC.AD∥BC,根据平行线的性质得到∠DAC=∠BCF,推出△ADE≌△BCF,根据全等三角形的性质即可得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC.AD∥BC,
∴∠DAC=∠BCF,
在△ADE与△BCF中,$\left\{\begin{array}{l}{AD=BC}\\{∠DAC=∠BCF}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△BCF,
∴∠AED=∠CFB.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意平行四边形的对边平行且相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.等腰三角形的一边长为3cm,周长为19cm,则该三角形的腰长为( )
| A. | 3cm | B. | 8cm | C. | 3cm或8cm | D. | 以上答案均不对 |
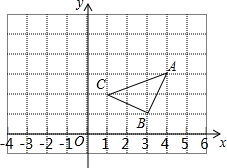 平面直角坐标系中的三是角形ABC如图所示,若三角形A1B1C1是由三角形ABC平移后得到的,且三角形ABC中的任意一点P(x,y)经过平移后的对应点为P1(x-3,y-5),
平面直角坐标系中的三是角形ABC如图所示,若三角形A1B1C1是由三角形ABC平移后得到的,且三角形ABC中的任意一点P(x,y)经过平移后的对应点为P1(x-3,y-5),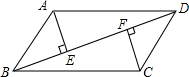 如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.
如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.