题目内容
4.下列式子中是代数式$\frac{y}{2}$,a-5,$\frac{2}{y}$,4a2b,-6,a2+3ab+b2,a,$\frac{3}{π}$,-x,0;是单项式$\frac{y}{2}$,4a2b,-6,a,$\frac{3}{π}$,-x,0;是整式$\frac{y}{2}$,a-5,4a2b,-6,a2+3ab+b2,a,$\frac{3}{π}$,-x,0;是多项式a-5,a2+3ab+b2.$\frac{y}{2}$,a-5,$\frac{2}{y}$,4a2b,-6,a2+3ab+b2,a,x=1,$\frac{3}{π}$,-x,$\frac{1}{2}>\frac{1}{3}$,0.
分析 根据代数式:代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子.单独的一个数或者一个字母也是代数式.带有“<(≤)”“>(≥)”“=”“≠”等符号的不是代数式;单项式的定义:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式;几个单项式的和叫做多项式;单项式和多项式统称为整式进行分析即可.
解答 解:代数式$\frac{y}{2}$,a-5,$\frac{2}{y}$,4a2b,-6,a2+3ab+b2,a,$\frac{3}{π}$,-x,0;
单项式$\frac{y}{2}$,4a2b,-6,a,$\frac{3}{π}$,-x,0;
整式$\frac{y}{2}$,a-5,4a2b,-6,a2+3ab+b2,a,$\frac{3}{π}$,-x,0;
多项式a-5,a2+3ab+b2.
故答案为:$\frac{y}{2}$,a-5,$\frac{2}{y}$,4a2b,-6,a2+3ab+b2,a,$\frac{3}{π}$,-x,0;$\frac{y}{2}$,4a2b,-6,a,$\frac{3}{π}$,-x,0;$\frac{y}{2}$,a-5,4a2b,-6,a2+3ab+b2,a,$\frac{3}{π}$,-x,0;a-5,a2+3ab+b2.
点评 此题主要考查了整式、代数式、单项式、多项式,关键是掌握整式、代数式、单项式、多项式的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.把抛物线y=-4x2先向上平移2个单位,再向左平移3个单位,所得的抛物线为( )
| A. | y=-4(x+3)2-2 | B. | y=-4(x+3)2+2 | C. | y=-4(x-3)2-2 | D. | y=-4(x-3)2+2 |
13. 如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )
如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )
 如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )
如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
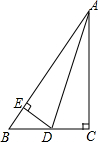 如图,AC⊥BD,AD平分∠BAC,DE⊥AB.试判断下面四个结论中哪些成立,哪些不成立.成立的,请说明理由;不成立的,请你在原有条件基础上再添加条件使之成立,并证明.(1)AD平分∠CDE;(2)∠BAC=∠BDE;(3)DE平分∠ADB;(4)BD+AC>AB.
如图,AC⊥BD,AD平分∠BAC,DE⊥AB.试判断下面四个结论中哪些成立,哪些不成立.成立的,请说明理由;不成立的,请你在原有条件基础上再添加条件使之成立,并证明.(1)AD平分∠CDE;(2)∠BAC=∠BDE;(3)DE平分∠ADB;(4)BD+AC>AB.