题目内容
4.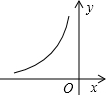 如图,是反比例函数y=$\frac{1-m}{x}$的图象中的一支,请回答
如图,是反比例函数y=$\frac{1-m}{x}$的图象中的一支,请回答(1)另一支在第四象限.
(2)m的取值范围为m<1.
(3)点A(-2,y1)和B(-1,y2)都在该图象上,则y1<y2(填>或<或=)
(4)若直线y=-x与图象交于点P,且线段OP=6,则m=19.
分析 (1)直接根据反比例函数的图象关于原点对称即可得出结论;
(2)根据反比例函数的图象与系数的关系即可得出结论;
(3)根据反比例函数的增减性即可得出结论;
(4)设P(a,-a)求出a的值,进而可得出P点坐标,代入反比例函数的解析式即可得出结论.
解答 解:(1)∵反比例函数的图象关于原点对称,
∴另一支在第三象限.
故答案为:四;
(2)∵反比例函数的图象在第二象限,
∴1-m<0,解得m<1.
故答案为:m<1;
(3)∵点A(-2,y1)和B(-1,y2)都在该图象上,-2<-1,
∴y1<y2.
故答案为:<;
(4)设P(a,-a)(a<0),
∵OP=6,
∴$\sqrt{{a}^{2}+(-a)^{2}}$=-a$\sqrt{2}$=6,解得a=-3$\sqrt{2}$,
∴P(-3$\sqrt{3}$,3$\sqrt{2}$).
∴点P在反比例函数y=$\frac{1-m}{x}$上,
∴3$\sqrt{2}$•(-3$\sqrt{2}$)=1-m,解得m=19.
故答案为:19.
点评 本题考查的是反比例函数与一次函数的交点问题,熟知反比例函数的图象与系数的关系是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件不能判定△ABC是直角三角形的是( )
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |
12.(-5ab)2的化简结果是( )
| A. | -25ab2 | B. | 25a2b2 | C. | -25a2b2 | D. | 25a2b |
19.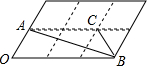 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |