题目内容
19.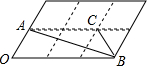 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 如图,连接EA、EC,先证明∠AEC=90°,E、C、B共线,再根据tan∠ABC=$\frac{AE}{EB}$,求出AE、EB即可解决问题.
解答  解:如图,连接EA,EC,
解:如图,连接EA,EC,
设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AE=$\sqrt{3}$a,EB=2a,
∴∠AEC=90°,
∵∠ACE=∠ACG=∠BCG=60°,
∴∠ECB=180°,
∴E、C、B共线,
在Rt△AEB中,tan∠ABC=$\frac{AE}{EB}$=$\frac{\sqrt{3}a}{2a}$=$\frac{\sqrt{3}}{2}$.
故选A.
点评 本题考查菱形的性质,三角函数、特殊三角形边角关系等知识,解题的关键是添加辅助线构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
9.从多边形的一个顶点出发,连接其它各个顶点得到2016个三角形,则这个多边形的边数为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
10.(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)可以表示为( )
| A. | (-$\frac{2}{3}$)×4 | B. | -$\frac{{2}^{4}}{3}$ | C. | -($\frac{2}{3}$)4 | D. | (-$\frac{2}{3}$)4 |
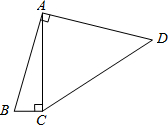 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?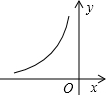 如图,是反比例函数y=$\frac{1-m}{x}$的图象中的一支,请回答
如图,是反比例函数y=$\frac{1-m}{x}$的图象中的一支,请回答
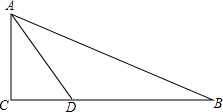 如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上,求DC的长.
如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上,求DC的长.