题目内容
15.两图均是4×4的正方形网格,格点A,格点B和直线l的位置如图所示,点P在直线l上.(1)请分别在图1和图2中作出点P,使PA+PB最短;
(2)请分别在图3和图4中作出点P,使PA-PB最长.
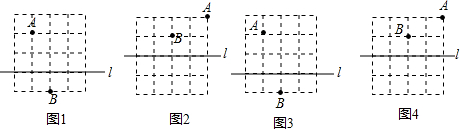
分析 (1)图1,根据两点之间线段最短,连接AB与直线l的交点即为点P,图2,找出点B关于直线l的对称点,连接AB′与直线l相交于点P,根据轴对称确定最短路线问题,点P即为所求;
(2)图3,找出点B关于直线l的对称点B′,连接AB′并延长与直线l相交于点P,根据轴对称的性质,PB=PB′,此时,点P即为所求;图4,连接AB并延长与直线l相交于点P,点P即为所求.
解答 解:如图所示.
点评 本题考查了轴对称确定最短路线问题,两点之间线段最短的性质,熟练掌握最短距离的确定方法是解题的关键.

练习册系列答案
相关题目
3.下列说法:
①若三角形一边上的中线和这边上的高重合,则这个三角形是等腰三角形;
②全等三角形的中线相等;
③如果直角三角形的两边长分别为3、4,那么斜边长为5;
④两条直角边对应相等的两个直角三角形全等.
其中正确的说法有( )
①若三角形一边上的中线和这边上的高重合,则这个三角形是等腰三角形;
②全等三角形的中线相等;
③如果直角三角形的两边长分别为3、4,那么斜边长为5;
④两条直角边对应相等的两个直角三角形全等.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)可以表示为( )
| A. | (-$\frac{2}{3}$)×4 | B. | -$\frac{{2}^{4}}{3}$ | C. | -($\frac{2}{3}$)4 | D. | (-$\frac{2}{3}$)4 |
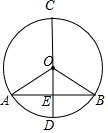 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,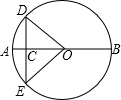 如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.
如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.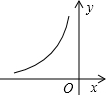 如图,是反比例函数y=$\frac{1-m}{x}$的图象中的一支,请回答
如图,是反比例函数y=$\frac{1-m}{x}$的图象中的一支,请回答