题目内容
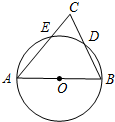 如图,AB为⊙O的直径,AC交⊙O于点E,BC交⊙O于点D,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③
如图,AB为⊙O的直径,AC交⊙O于点E,BC交⊙O于点D,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③ |
| AE |
 |
| BE |
其中正确结论的序号是
考点:圆周角定理,相似三角形的判定与性质
专题:
分析:连结AD、BE,DE,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,加上CD=BD,根据等腰三角形的判定即可得到AB=AC;再根据等腰三角形的性质和三角形内角和定理可计算出∠BAC=40°;由AB为直径得到∠AEB=90°,则∠ABE=50°,根据圆周角定理可判断
≠
;接着证明△CED∽△CBA,利用相似比得到CE•CA=CD•CB,然后利用等线段代换即可得到CE•CA=2BD2.
 |
| AE |
 |
| BE |
解答: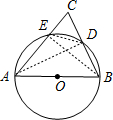 解:连结AD、BE,DE,如图,
解:连结AD、BE,DE,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
而CD=BD,
∴AB=AC,所以②正确;
∵∠C=70°,
∴∠ABC=∠C=70°,
∴∠BAC=40°,所以①错误;
∵AB为直径,
∴∠AEB=90°,
∴∠ABE=50°,
∴
≠
,所以③错误;
∵∠CED=∠CBA,
而∠C公共,
∴△CED∽△CBA,
∴
=
,
∴CE•CA=CD•CB,
∴CE•CA=BD•2BD=2BD2,所以④正确.
故答案为②④.
 解:连结AD、BE,DE,如图,
解:连结AD、BE,DE,如图,∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
而CD=BD,
∴AB=AC,所以②正确;
∵∠C=70°,
∴∠ABC=∠C=70°,
∴∠BAC=40°,所以①错误;
∵AB为直径,
∴∠AEB=90°,
∴∠ABE=50°,
∴
 |
| AE |
 |
| BE |
∵∠CED=∠CBA,
而∠C公共,
∴△CED∽△CBA,
∴
| CE |
| CB |
| CD |
| CA |
∴CE•CA=CD•CB,
∴CE•CA=BD•2BD=2BD2,所以④正确.
故答案为②④.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一定点P与圆周上点的最大距离为6cm,最小距离为2cm,则此圆的半径为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、8cm或4cm |
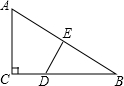 如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于点D,交AB于点E.当∠B=30°时,下列结论不正确的是( )
如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于点D,交AB于点E.当∠B=30°时,下列结论不正确的是( )| A、AC=AE=BE |
| B、AD=BD |
| C、CD=BD |
| D、CE=BE |
已知
=
,那么
、
、
的大小关系是( )
| a+b |
| b |
| 7 |
| 3 |
| a |
| b |
| a-b |
| b |
| a+b |
| a-b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,已知⊙O的半径为2cm,弦AB=2cm,P点为弦AB上一动点,则线段OP的范围是
如图,已知⊙O的半径为2cm,弦AB=2cm,P点为弦AB上一动点,则线段OP的范围是 已知:如图∠ABC=∠ACB,AD平分∠BAC,点P在直线AD上,求证:PB=PC.
已知:如图∠ABC=∠ACB,AD平分∠BAC,点P在直线AD上,求证:PB=PC.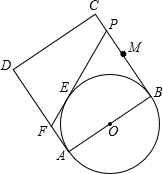 已知正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点,P不与M和C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.求四边形CDFP的周长.
已知正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点,P不与M和C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.求四边形CDFP的周长.