题目内容
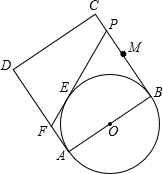已知正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点，P不与M和C重合，以AB为直径作⊙O，过点P作⊙O的切线交AD于点F，切点为E．求四边形CDFP的周长．考点：切线长定理
专题：
分析：利用切线长定理得出四边形CDFP的周长为AD+DC+CB即可得出答案．
解答：解：∵四边形ABCD是正方形，
∴∠A=∠B=90°，
∴OA⊥AD，OB⊥BC，
∵OA，OB是半径，
∴AF、BP都是⊙O的切线，
又∵PF是⊙O的切线，
∴FE=FA，PE=PB，
∴四边形CDFP的周长为AD+DC+CB=2×3=6．
∴∠A=∠B=90°，
∴OA⊥AD，OB⊥BC，
∵OA，OB是半径，
∴AF、BP都是⊙O的切线，
又∵PF是⊙O的切线，
∴FE=FA，PE=PB，
∴四边形CDFP的周长为AD+DC+CB=2×3=6．
点评：此题主要考查了切线长定理，得出四边形CDFP的周长为AD+DC+CB是解题关键．
练习册系列答案
相关题目
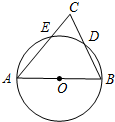如图，AB为⊙O的直径，AC交⊙O于点E，BC交⊙O于点D，CD=BD，∠C=70°．现给出以下四个结论：①∠A=45°；②AC=AB；③
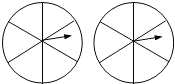如图，用两个相同的转盘（每个圆都平均分成六个扇形）玩配紫色游戏（-个转盘转出“红”，另一个转盘转出“蓝”，则为配成紫色）．在所给转盘中的扇形里，分别填上“红”或“蓝”，使得到紫色的概率是
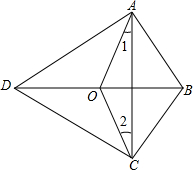如图，在四边形ABCD中，∠BAD=∠BCD=90°，点O是BD的中点．求证：∠1=∠2．
已知：如图，在△ABC中，边AB，BC的垂直平分线交于P．求证：PA=PB=PC．
画出右上方图形关于直线l的对称图形．