题目内容
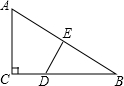 如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于点D,交AB于点E.当∠B=30°时,下列结论不正确的是( )
如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于点D,交AB于点E.当∠B=30°时,下列结论不正确的是( )| A、AC=AE=BE |
| B、AD=BD |
| C、CD=BD |
| D、CE=BE |
考点:线段垂直平分线的性质,含30度角的直角三角形
专题:
分析:根据线段垂直平分线性质得出AD=BD,AE=BE,DE⊥AB,求出∠DAB=∠B=30°,∠CAD=30°,根据角平分线性质求出AC=AE,根据直角三角形斜边上中线性质求出CE=BE,即可得出选项.
解答:解:
连接AD,
∵AB的垂直平分线DE,
∴AD=BD,
∴∠B=∠DAB=30°,
∴∠CAD=180°-90°-30°-30°=30°,
∴∠CAD=∠EAD=30°,
∵∠ACB=90°,DE⊥AB,
∴AC=AE=BE,
∵AE=BE,△ACB是直角三角形,
∴CE=BE=AE,
即选项A、B、D正确;
∵CD<AD,AD=BD,
∴CD<BD,
即选项C错误;
故选C.

连接AD,
∵AB的垂直平分线DE,
∴AD=BD,
∴∠B=∠DAB=30°,
∴∠CAD=180°-90°-30°-30°=30°,
∴∠CAD=∠EAD=30°,
∵∠ACB=90°,DE⊥AB,
∴AC=AE=BE,
∵AE=BE,△ACB是直角三角形,
∴CE=BE=AE,
即选项A、B、D正确;
∵CD<AD,AD=BD,
∴CD<BD,
即选项C错误;
故选C.
点评:本题考查了直角三角形斜边上中线性质,角平分线性质,线段垂直平分线性质等性质的应用,能综合运用性质进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
在下列图形中,不是轴对称图形的是( )
| A、一条线段 |
| B、一个角 |
| C、一个平行四边形 |
| D、一个等腰梯形 |
 已知:如图,在△ABC中.O是∠ABC、∠CAB外角的平分线的交点,那么点O在∠C的平分线上吗?为什么?
已知:如图,在△ABC中.O是∠ABC、∠CAB外角的平分线的交点,那么点O在∠C的平分线上吗?为什么?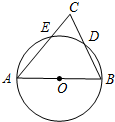 如图,AB为⊙O的直径,AC交⊙O于点E,BC交⊙O于点D,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③
如图,AB为⊙O的直径,AC交⊙O于点E,BC交⊙O于点D,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③
 已知抛物线y=x2-4与y轴交于点A,与x轴分别交于B、C两点,将该抛物线分别平移后得到抛物线l1,l2,其中l1的顶点为点B,l2的顶点为点C,则有这三条抛物线所围成的图形(图中阴影部分)的面积为( )
已知抛物线y=x2-4与y轴交于点A,与x轴分别交于B、C两点,将该抛物线分别平移后得到抛物线l1,l2,其中l1的顶点为点B,l2的顶点为点C,则有这三条抛物线所围成的图形(图中阴影部分)的面积为( ) 已知:如图,在△ABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
已知:如图,在△ABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.