题目内容
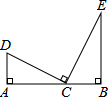 如图,AD⊥AB,BE⊥AB,点C在AB上,连接CD,CE,若CD⊥CE,CD=CE,AD=3cm,BE=5cm,则△ACD与△BCE的面积之和为
如图,AD⊥AB,BE⊥AB,点C在AB上,连接CD,CE,若CD⊥CE,CD=CE,AD=3cm,BE=5cm,则△ACD与△BCE的面积之和为考点:全等三角形的判定与性质
专题:
分析:求出A=∠B=∠DCE=90°,∠D=∠BCE,根据AAS推出△DAC≌△CBE,根据全等三角形的性质得出AD=BC,BE=AC,根据三角形的面积公式求出即可.
解答:解:∵AD⊥AB,BE⊥AB,CD⊥CE,
∴∠A=∠B=∠DCE=90°,
∴∠D+∠DCA=90°,∠DCA=∠BCE=90°,
∴∠D=∠BCE,
在△DAC和△CBE中,
,
∴△DAC≌△CBE(AAS),
∴AD=BC,BE=AC,
∵AD=3cm,BE=5cm,
∴BC=3cm,AC=5cm,
∴△ACD与△BCE的面积之和为
×3cm×5cm×2=15cm2,
故答案为:15.
∴∠A=∠B=∠DCE=90°,
∴∠D+∠DCA=90°,∠DCA=∠BCE=90°,
∴∠D=∠BCE,
在△DAC和△CBE中,
|
∴△DAC≌△CBE(AAS),
∴AD=BC,BE=AC,
∵AD=3cm,BE=5cm,
∴BC=3cm,AC=5cm,
∴△ACD与△BCE的面积之和为
| 1 |
| 2 |
故答案为:15.
点评:本题考查了三角形内角和定理,垂直定义,全等三角形的性质和判定的应用,解此题的关键是推出△DAC≌△CBE,难度适中.

练习册系列答案
相关题目
下列方程中,属于一元一次方程的是( )
| A、x-3 |
| B、x=-2x2-1=0 |
| C、2x-3=0 |
| D、x-y=3 |
若等腰梯形的面积为160cm2,上底比高长4cm,下底比高长20cm,则这个梯形的高为( )
| A、8cm |
| B、20cm |
| C、8cm或20cm |
| D、以上都不对 |
 如图,在平行四边形ABCD中,若∠B=100°,那么∠A、∠D的度数分别是( )度.
如图,在平行四边形ABCD中,若∠B=100°,那么∠A、∠D的度数分别是( )度.| A、80、100 |
| B、100、80 |
| C、80、80 |
| D、100、100 |
 如图,在锐角△ABC中,∠A=50°,AC、BC两边的垂直平分线交于点O,则∠BOC的度数是( )
如图,在锐角△ABC中,∠A=50°,AC、BC两边的垂直平分线交于点O,则∠BOC的度数是( )| A、40° | B、50° |
| C、100° | D、120° |
 △ABC中,AB=AC=5,BC=6,建立适当的直角坐标系,并写出点A、B、C的坐标.
△ABC中,AB=AC=5,BC=6,建立适当的直角坐标系,并写出点A、B、C的坐标. 如图所示,∠1+∠2+∠3+∠4等于
如图所示,∠1+∠2+∠3+∠4等于 如图所示,15只空油桶堆在一起,每只油桶的底面直径均为50厘米.现在要给它们盖一个遮雨棚,遮雨棚起码要多高?(结果精确到0.01厘米)
如图所示,15只空油桶堆在一起,每只油桶的底面直径均为50厘米.现在要给它们盖一个遮雨棚,遮雨棚起码要多高?(结果精确到0.01厘米) 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.