题目内容
 如图,在锐角△ABC中,∠A=50°,AC、BC两边的垂直平分线交于点O,则∠BOC的度数是( )
如图,在锐角△ABC中,∠A=50°,AC、BC两边的垂直平分线交于点O,则∠BOC的度数是( )| A、40° | B、50° |
| C、100° | D、120° |
考点:线段垂直平分线的性质
专题:计算题
分析:先根据线段垂直平分线的性得OB=OC,OC=OA,则OA=OB,于是根据等腰三角形的性质得∠OAB=∠4,∠OAC=∠2,所以∠2+∠4=∠BAC=50°,再根据三角形内角和定理得∠ABC+∠ACB=130°,则∠1+∠3=80°,然后再根据三角形内角和计算∠BOC的度数.
解答:解:连结OA,如图,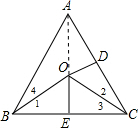
∵AC、BC两边的垂直平分线交于点O,
∴OB=OC,OC=OA,
∴OA=OB,
∴∠OAB=∠4,∠OAC=∠2,
∴∠2+∠4=∠OAC+∠OAB=∠BAC=50°,
∵∠ABC+∠ACB=180°-∠BAC=130°,
∴∠1+∠3=130°-(∠2+∠4)=80°,
∴∠BOC=180°-(∠1+∠3)=100°.
故选C.

∵AC、BC两边的垂直平分线交于点O,
∴OB=OC,OC=OA,
∴OA=OB,
∴∠OAB=∠4,∠OAC=∠2,
∴∠2+∠4=∠OAC+∠OAB=∠BAC=50°,
∵∠ABC+∠ACB=180°-∠BAC=130°,
∴∠1+∠3=130°-(∠2+∠4)=80°,
∴∠BOC=180°-(∠1+∠3)=100°.
故选C.
点评:本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等.解题的关键是利用等腰三角形的性质和三角形内角和定理.

练习册系列答案
相关题目
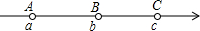 如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点B与点C之间(靠近点C)或点C的右边 |
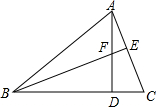 △ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )
△ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )| A、2 | B、3 | C、4 | D、5 |
函数值y随x的增大而减小的是( )
| A、y=1+x | ||
B、y=
| ||
| C、y=-x+1 | ||
| D、y=-2+3x |
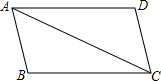 如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )
如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )| A、SAS | B、ASA |
| C、AAS | D、以上都不对 |
下列说法中,正确的是( )
| A、一个数的立方根有两个,它们互为相反数 |
| B、负数没有立方根 |
| C、一个数的立方根比平方根小 |
| D、0的立方根仍为0 |
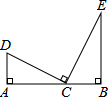 如图,AD⊥AB,BE⊥AB,点C在AB上,连接CD,CE,若CD⊥CE,CD=CE,AD=3cm,BE=5cm,则△ACD与△BCE的面积之和为
如图,AD⊥AB,BE⊥AB,点C在AB上,连接CD,CE,若CD⊥CE,CD=CE,AD=3cm,BE=5cm,则△ACD与△BCE的面积之和为 小明写作业时,不慎将墨水滴在数轴上,根据图中数值,请你确定墨迹盖住部分的整数共有
小明写作业时,不慎将墨水滴在数轴上,根据图中数值,请你确定墨迹盖住部分的整数共有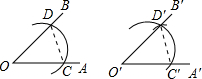 如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC.由这种作图方法得到的△D′O′C′和△DOC全等的依据是
如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC.由这种作图方法得到的△D′O′C′和△DOC全等的依据是