题目内容
 △ABC中,AB=AC=5,BC=6,建立适当的直角坐标系,并写出点A、B、C的坐标.
△ABC中,AB=AC=5,BC=6,建立适当的直角坐标系,并写出点A、B、C的坐标.考点:坐标与图形性质,等腰三角形的性质
专题:开放型
分析:作AO⊥BC,以点O为原点建立直角坐标系,如图,根据等腰三角形的性质得OB=OC=
BC=3,再利用勾股定理计算出OA=4,然后利用坐标轴上点的坐标特征写出点A、B、C的坐标.
| 1 |
| 2 |
解答:解:作AO⊥BC,以点O为原点建立直角坐标系,如图,
∵AB=AC=5,
∴OB=OC=
BC=3,
在Rt△AOB中,∵AB=5,OB=3,
∴OA=
=4,
∴A点坐标为(0,4),B点坐标为(-3,0),C点坐标为(3,0).

∵AB=AC=5,
∴OB=OC=
| 1 |
| 2 |
在Rt△AOB中,∵AB=5,OB=3,
∴OA=
| AB2-OB2 |
∴A点坐标为(0,4),B点坐标为(-3,0),C点坐标为(3,0).
点评:本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了等腰三角形的性质.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知三角形两边长分别为3和8,第三边的长为方程x2-14x+48=0的一根,则这个三角形的周长为( )
| A、11 | B、17 |
| C、17或19 | D、19 |
 已知⊙O中弦AB、CD相交于点P,PO平分∠APD,则下列结论中不正确的是( )
已知⊙O中弦AB、CD相交于点P,PO平分∠APD,则下列结论中不正确的是( )| A、AB=CD | ||||
B、
| ||||
| C、PA=PD | ||||
D、
|
下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )
A、 |
B、 |
C、 |
D、 |
 如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点B与点C之间(靠近点C)或点C的右边 |


 如图,有一块三角形土地,AC=6m,BC=4m,∠B=60°,则这块土地的面积为
如图,有一块三角形土地,AC=6m,BC=4m,∠B=60°,则这块土地的面积为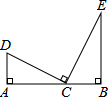 如图,AD⊥AB,BE⊥AB,点C在AB上,连接CD,CE,若CD⊥CE,CD=CE,AD=3cm,BE=5cm,则△ACD与△BCE的面积之和为
如图,AD⊥AB,BE⊥AB,点C在AB上,连接CD,CE,若CD⊥CE,CD=CE,AD=3cm,BE=5cm,则△ACD与△BCE的面积之和为