题目内容
 如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是
如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是考点:角平分线的性质
专题:
分析:先根据角平分线的性质得出DE=DF,再由三角形的面积公式即可得出结论.
解答:解:∵如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,
∴DE=DF.
∵S△ABC=30,AB=18,BC=12,
∴S△ABD+S△BCD=
AB•DE+
BC•DF=30,即
×18DE+
×12DE=30,解得DE=2.
故答案为:2.
∴DE=DF.
∵S△ABC=30,AB=18,BC=12,
∴S△ABD+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
计算2x3÷x3,正确的是( )
| A、2 | B、1 | C、x | D、2x |
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,AB=13,AC=5,以点C为圆心,
如图,在Rt△ABC中,∠C=90°,CD⊥AB,AB=13,AC=5,以点C为圆心, 一次函数y=kx+b图象经过点(0,3)和(4,6).
一次函数y=kx+b图象经过点(0,3)和(4,6).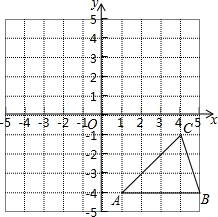 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格上,点C的坐标为(4,-1),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格上,点C的坐标为(4,-1),