题目内容
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,AB=13,AC=5,以点C为圆心,
如图,在Rt△ABC中,∠C=90°,CD⊥AB,AB=13,AC=5,以点C为圆心,| 60 |
| 13 |
考点:点与圆的位置关系
专题:计算题
分析:先利用勾股定理计算出BC=12,再利用面积法计算出CD,然后根据点与圆的位置关系的判定方法进行判断.
解答:解:在Rt△ACB中,∵AB=13,AC=5,
∴BC=
=12,
∵
•CD•AB=
BC•AC,
∴CD=
=
,
∵BC>CD,AC>CD,
∴A点和B点在以点C为圆心,
为半径的圆外,D点在以点C为圆心,
为半径的圆上.
∴BC=
| AB2-AC2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 5×12 |
| 13 |
| 60 |
| 13 |
∵BC>CD,AC>CD,
∴A点和B点在以点C为圆心,
| 60 |
| 13 |
| 60 |
| 13 |
点评:本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外?d>r;点P在圆上?d=r;点P在圆内?d<r.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在数轴上与表示-3的点的距离等于5的点所表示的数是( )
| A、-8和2 | B、8和-2 |
| C、-8和-2 | D、8和2 |
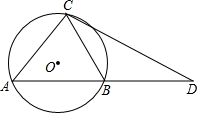 如图,A、C为⊙O上两点,DA交⊙O于点B,连接AC、BC,若∠DCB=∠A,直线CD与⊙O相切吗?证明你的结论.
如图,A、C为⊙O上两点,DA交⊙O于点B,连接AC、BC,若∠DCB=∠A,直线CD与⊙O相切吗?证明你的结论. 如图,在△ABC中,AB=AC,D为BC边上一点,连接AD并延长,与三角形ABC的外接圆交于点E.
如图,在△ABC中,AB=AC,D为BC边上一点,连接AD并延长,与三角形ABC的外接圆交于点E. 如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是
如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是