题目内容
如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以ED为折痕向右折叠,AE与BC交于点F,则CF为( )

| A、2 | B、3 | C、4 | D、5 |
考点:翻折变换(折叠问题)
专题:
分析:首先根据翻折变换的性质求出图中的线段AB、AD等的长度;证明△ABF∽△ECF,列出比例式即可解决问题.
解答:解:从左到右三个图形依次记为图1、图2、图3;

由题意知:
在图2中,AD=6,BD=10-6=4,EC=BD=4;
在图3中,AB=AD-BD=6-4=2;
设CF=x,则BF=6-x;
∵△ABF∽△ECF,
∴
=
,即
=
,
解得:x=4,
故答案为:4.

由题意知:
在图2中,AD=6,BD=10-6=4,EC=BD=4;
在图3中,AB=AD-BD=6-4=2;
设CF=x,则BF=6-x;
∵△ABF∽△ECF,
∴
| AB |
| EC |
| BF |
| CF |
| 2 |
| 4 |
| 6-x |
| x |
解得:x=4,
故答案为:4.
点评:该命题以矩形为载体,以翻折变换为方法,以考查翻折变换的性质及其应用为核心构造而成;解题的关键是利用翻折变换的性质准确找出图中隐含的等量关系,灵活分析、判断或证明.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是
如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是 如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大?
如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大?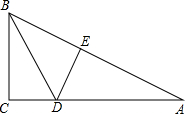 已知,如图,△ABC中,∠C=90°,AB=10,AC=8,BD为∠ABC的角平分线交AC于D,过点D作DE垂直AB于点E,
已知,如图,△ABC中,∠C=90°,AB=10,AC=8,BD为∠ABC的角平分线交AC于D,过点D作DE垂直AB于点E,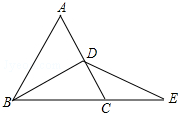 已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.
已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE. 如图,∠APB=30°,O点在PB上,⊙O的半径为1cm,OP=6cm,若⊙O在直线BP上延BP方向以每秒2cm的速度平移,当圆心O平移
如图,∠APB=30°,O点在PB上,⊙O的半径为1cm,OP=6cm,若⊙O在直线BP上延BP方向以每秒2cm的速度平移,当圆心O平移