题目内容
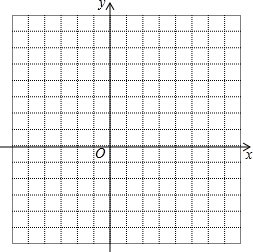 一次函数y=kx+b图象经过点(0,3)和(4,6).
一次函数y=kx+b图象经过点(0,3)和(4,6).①画出这个一次函数图象;
②当x
③试求该函数的关系式;
④若图象与x轴的交点为A,与y轴的交点为B,求△AOB的面积.
考点:一次函数的图象,一次函数的性质
专题:
分析:①利用两点法作出一次函数图象即可;
②根据函数图象写出x轴上方部分的x的取值范围即可;
③利用待定系数法求一次函数解析式解答;
④求出OA、OB,然后利用三角形的面积公式列式计算即可得解.
②根据函数图象写出x轴上方部分的x的取值范围即可;
③利用待定系数法求一次函数解析式解答;
④求出OA、OB,然后利用三角形的面积公式列式计算即可得解.
解答: 解:①如图所示;
解:①如图所示;
②x>-4时,y>0;
故答案为:x>-4;
③∵一次函数y=kx+b图象经过点(0,3)和(4,6)
∴b=3,且4k+b=6,
∴k=
,
∴该函数的关系式为y=
x+3;
④令y=0,则
x+3=0,
解得x=-4,
则点A的坐标为(-4,0),得OA=4,
令x=0,则y=3,
则点B的坐标为(0,3),得OB=3,
∴S△AOB=
OA•OB=
×3×4=6.
 解:①如图所示;
解:①如图所示;②x>-4时,y>0;
故答案为:x>-4;
③∵一次函数y=kx+b图象经过点(0,3)和(4,6)
∴b=3,且4k+b=6,
∴k=
| 3 |
| 4 |
∴该函数的关系式为y=
| 3 |
| 4 |
④令y=0,则
| 3 |
| 4 |
解得x=-4,
则点A的坐标为(-4,0),得OA=4,
令x=0,则y=3,
则点B的坐标为(0,3),得OB=3,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数图象,一次函数与不等式,待定系数法求一次函数解析式,三角形的面积,是基础题,综合掌握一次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AB=AC,D为BC边上一点,连接AD并延长,与三角形ABC的外接圆交于点E.
如图,在△ABC中,AB=AC,D为BC边上一点,连接AD并延长,与三角形ABC的外接圆交于点E. 如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是
如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,若S△ABC=30,AB=18,BC=12,则DE的长是
 如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大?
如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大?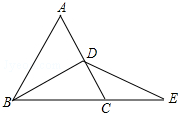 已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.
已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.