题目内容
3.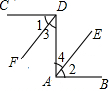 已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.证明:∵CD⊥DA,DA⊥AB,(已知)
∴∠CDA=∠DAB=90°.(垂直定义)
又∠1=∠2,已知
∴∠CDA-∠1=∠DAB-∠2,(等式的性质)
即∠3=∠4.
∴DF∥AE.(内错角相等,两直线平行)
分析 根据已知条件、以及平行线的判定进行填空即可.
解答 证明:∵CD⊥DA,DA⊥AB,(已知)
∴∠CDA=∠DAB=90°.(垂直定义)
又∠1=∠2,(已知)
∴∠CDA-∠1=∠DAB-∠2,(等式的性质)
即∠3=∠4.
∴DF∥AE.(内错角相等,两直线平行).
故答案分别为:已知,垂直的定义,已知,等式的性质,内错角相等,两直线平行.
点评 本题考查平行线的判定、垂线的定义等知识,熟练掌握平行线的判定是解决问题的关键,学会利用等式性质证明角相等,属于基础题.

练习册系列答案
相关题目
18.正方形的边长是2,它的对角线长为( )
| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
15.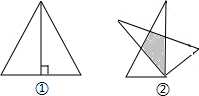 如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )
如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )
 如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )
如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )| A. | ($\sqrt{3}$-1)cm | B. | 2cm | C. | ($\sqrt{3}$+1)cm | D. | 无法确定 |
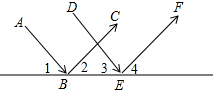 如图,平行光线AB与DE射向同一平面镜后被反射,此时∠1=∠2,∠3=∠4,那么反射光线BC与EF平行吗?说明理由.
如图,平行光线AB与DE射向同一平面镜后被反射,此时∠1=∠2,∠3=∠4,那么反射光线BC与EF平行吗?说明理由.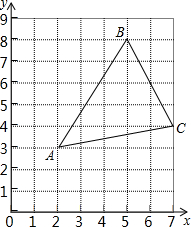 如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.
如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.