题目内容
12.判断代数式($\frac{2{a}^{2}+2a}{{a}^{2}-1}-\frac{{a}^{2}-a}{{a}^{2}-2a+1}$)$÷\frac{a}{a+1}$的值能否等于-1?并说明理由.分析 先将原代数式化简,再令化简后的结果等于-1,解出a的值,由结合分式存在的意义可以得出结论.
解答 解:原式=[$\frac{2a(a+1)}{(a+1)(a-1)}$-$\frac{a(a-1)}{(a-1)^{2}}$]×$\frac{a+1}{a}$,
=$\frac{2a-a}{a-1}$×$\frac{a+1}{a}$,
=$\frac{a+1}{a-1}$.
当$\frac{a+1}{a-1}$=-1时,解得:a=0,
∵(a+1)(a-1)a≠0,即a≠±1,a≠0,
∴代数式($\frac{2{a}^{2}+2a}{{a}^{2}-1}-\frac{{a}^{2}-a}{{a}^{2}-2a+1}$)$÷\frac{a}{a+1}$的值不能等于-1.
点评 本题考查了分式的化简求值和分式存在的意义,解题的关键:将原式化简后令其=-1,解得a=0,再去判定分母是否为0.本题属于基础题型,解决该类题型时一定要注意分母不能为0.

练习册系列答案
相关题目
7.已知抛物线y=ax2+bx+c的开口向上,顶点坐标为(3,-2),那么该抛物线有( )
| A. | 最小值-2 | B. | 最大值-2 | C. | 最小值3 | D. | 最大值3 |
1.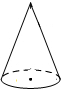 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )| A. | 圆锥的底面半径为3 | B. | tanα=$\frac{\sqrt{2}}{2}$ | ||
| C. | 圆锥的表面积为12π | D. | 该圆锥的主视图的面积为8$\sqrt{2}$ |
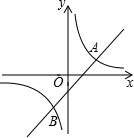 在平面直角坐标系中,直线y1=x+m与双曲线y2=$\frac{k}{x}$交于点A、B,已知点A、B的横坐标为2和-1.
在平面直角坐标系中,直线y1=x+m与双曲线y2=$\frac{k}{x}$交于点A、B,已知点A、B的横坐标为2和-1.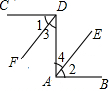 已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.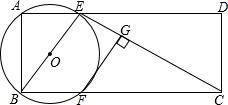 如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.
如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.