题目内容
13.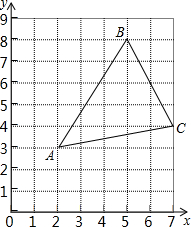 如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.
如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.(1)点C用有序数对表示为(7,4).
(2)试求出三角形ABC的面积.
分析 (1)由图可知点C的坐标;
(2)求△ABC的面积可利用割补法,将三角形向右补成一个直角梯形,用直角梯形面积减去两个直角三角形面积可得.
解答 解:(1)由图可知,点C坐标为(7,4);
(2)S△ABC=$\frac{1}{2}$×(2+5)×5-$\frac{1}{2}$×5×1-$\frac{1}{2}$×4×2
=11.
点评 本题主要考查坐标与图形的面积及割补法求三角形面积,将三角形割补成一个易求、规则的几何图形来求面积是割补法的关键.

练习册系列答案
相关题目
1.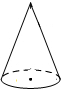 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )| A. | 圆锥的底面半径为3 | B. | tanα=$\frac{\sqrt{2}}{2}$ | ||
| C. | 圆锥的表面积为12π | D. | 该圆锥的主视图的面积为8$\sqrt{2}$ |
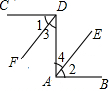 已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.