题目内容
8.等边三角形的边长为3,则该三角形的面积为$\frac{9\sqrt{3}}{4}$.分析 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
解答 解:等边三角形高线即中线,故D为BC中点,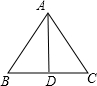
∵AB=3,
∴BD=1.5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\frac{3}{2}\sqrt{3}$,
∴等边△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×3×$\frac{3\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{4}$.
故答案为:$\frac{9\sqrt{3}}{4}$.
点评 本题考查了勾股定理在直角三角形中的运用,等边三角形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
16.某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对自己所任教的八年级(1)班和(2)班进行了检测.如下两组数据表示从两班各随机抽取的10名学生的得分情况:(单位:分)
(1)班:24,21,27,24,21,27,21,24,27,24.
(2)班:24,21,30,21,27,15,27,21,24,30.
(1)利用图中提供的信息,补全下表:
(2)若把24分以上记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀.
(1)班:24,21,27,24,21,27,21,24,27,24.
(2)班:24,21,30,21,27,15,27,21,24,30.
(1)利用图中提供的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | 24 |
| (2)班 | 24 | 24 | 21 |
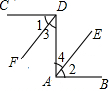 已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.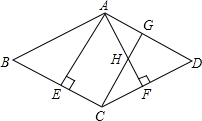 如图所示,菱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD,CG∥AE,CG交AF于点H,交AD于点G.
如图所示,菱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD,CG∥AE,CG交AF于点H,交AD于点G.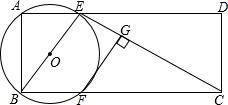 如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.
如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.