题目内容
16.点P为直线l外一点,点A、B、C为直线l上的三点,PA=4,PB=5,PC=2,则点P到直线l的距离为( )| A. | 2 | B. | 4 | C. | 不大于2 | D. | 小于2 |
分析 根据直线外一点到直线的垂线段的长度,叫做点到直线的距离,可得连结直线外一点P与直线上任意点,所得线段中垂线段最短;然后根据PA=4,PB=5,PC=2,可得三条线段的最短的是2,所以点P到直线l的距离不大于2,据此判断即可.
解答 解:连接直线外一点P与直线上任意点,所得线段中垂线段最短;
因为PA=4,PB=5,PC=2,
所以三条线段的最短的是2,
所以点P到直线l的距离不大于2.
故选:C.
点评 此题主要考查了点到直线的距离的含义以及特征,考查了分析推理能力的应用,解答此题的关键是要明确:连接直线外一点P与直线上任意点,所得线段中垂线段最短.

练习册系列答案
相关题目
11.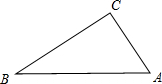 如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
 如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )| A. | 四边形CEDF为菱形 | B. | DE=DA | ||
| C. | DF⊥CB | D. | CD=BD |
8.在实数:3.14159,$\root{3}{64}$,1.010010001…,4.21,π,$\frac{22}{7}$,3$\sqrt{2}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 72° |
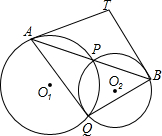 如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆. 已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论: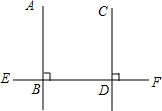 写出下列命题的已知、求证,并完成证明过程.
写出下列命题的已知、求证,并完成证明过程.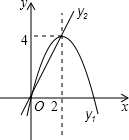 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.则①当x>4时,M<0;②当x<2时,M随着x增大而增大;③使得M大于4的x值不存在;④若M=2,则x=1,其中正确的有②③(填写序号)
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.则①当x>4时,M<0;②当x<2时,M随着x增大而增大;③使得M大于4的x值不存在;④若M=2,则x=1,其中正确的有②③(填写序号)