题目内容
11.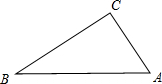 如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )| A. | 四边形CEDF为菱形 | B. | DE=DA | ||
| C. | DF⊥CB | D. | CD=BD |
分析 由线段的垂直平分线证出∠CGF=∠CGE=90°,CF=DF,CE=DE,再证明△CGF≌△CGE,得出CF=CE,证出CF=CE=DF=DE,即可证出四边形CEDF是菱形.
解答 解: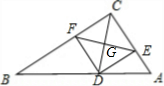 如图所示∵CD是∠ACB的平分线,
如图所示∵CD是∠ACB的平分线,
∴∠FCG=∠ECG,
∵EF是线段CD的垂直平分线,
∴∠CGF=∠CGE=90°,CF=DF,CE=DE,
在△CGF和△CGE中,$\left\{\begin{array}{l}{∠FCG=∠ECG}&{\;}\\{CG=CG}&{\;}\\{∠CGF=∠CGE}&{\;}\end{array}\right.$,
∴△CGF≌△CGE(ASA),
∴CF=CE,
∴CF=CE=DF=DE,
∴四边形CEDF是菱形,
∴A正确,B、C、D不正确;
故选:A.
点评 本题考查了作图-复杂、菱形的判定与性质、全等三角形的判定与性质、线段垂直平分线的性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2. 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 41 |
6. 如图,平行四边形ABCD中,点E是边AD的一个三等分点,EC交对角线BD于点F,则FC:EC等于( )
如图,平行四边形ABCD中,点E是边AD的一个三等分点,EC交对角线BD于点F,则FC:EC等于( )
 如图,平行四边形ABCD中,点E是边AD的一个三等分点,EC交对角线BD于点F,则FC:EC等于( )
如图,平行四边形ABCD中,点E是边AD的一个三等分点,EC交对角线BD于点F,则FC:EC等于( )| A. | 3:2 | B. | 3:4 | C. | 1:1 | D. | 1:2 |
16.点P为直线l外一点,点A、B、C为直线l上的三点,PA=4,PB=5,PC=2,则点P到直线l的距离为( )
| A. | 2 | B. | 4 | C. | 不大于2 | D. | 小于2 |
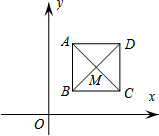 如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2).
如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2). 如图所示,数轴的正半轴上有A、B、C三点,表示1和$\sqrt{2}$的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.
如图所示,数轴的正半轴上有A、B、C三点,表示1和$\sqrt{2}$的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.