Question

1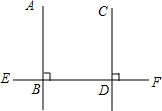．写出下列命题的已知、求证，并完成证明过程．
命题：在同一平面内，垂直于同一条直线的两条直线互相平行．
已知：如图，AB⊥EF，垂足为B，CD⊥EF，垂足为D．
求证：AB∥CD．
证明：∵AB⊥EF，CD⊥EF，
∴∠ABD=∠CDF=90°，
∴AB∥CD．．

Answer 1

分析 先将原命题改写成：如果…，那么…的形式，如果后面的是已知，那么后面的是求证，然后即可写出已知和求证，然后根据同位角相等两直线平行即可证明．

解答 原命题改写为：在同一平面内，如果两条直线垂直于同一条直线，那么这两条直线平行．
已知：如图，AB⊥EF，垂足为B，CD⊥EF，垂足为D．
求证：AB∥CD．
证明：∵AB⊥EF，CD⊥EF，
∴∠ABD=∠CDF=90°，
∴AB∥CD．

点评 本题主要考查学生对命题的定义的理解，难度适中，解题的关键是：先将原命题改写成：如果…，那么…的形式，然后写出已知和求证．