题目内容
7.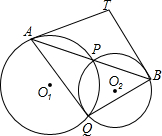 如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
分析 连接PQ,首先根据TA和TB分别与⊙O1与⊙O2切于点A和点B利用弦切角定理得到∠TAP=∠AQP,∠TBA=∠BQP,从而得到∠ATB+∠AQB=∠ATB+(∠AQP+∠BQP)=∠ATB+∠TAP+∠TBA=180°,证得T、A、Q、B四点共圆.
解答 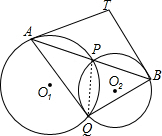 解:如图,连接PQ,
解:如图,连接PQ,
∵TA和TB分别与⊙O1与⊙O2切于点A和点B,
∴∠TAP=∠AQP,∠TBA=∠BQP,
∴∠ATB+∠AQB=∠ATB+(∠AQP+∠BQP)=∠ATB+∠TAP+∠TBA=180°,
∴T、A、Q、B四点共圆.
点评 本题考查了四点共圆的知识,解题的关键是了解要证明四点共圆证明其相对的两角的和为180°即可,难度不大.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2. 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 41 |
16.点P为直线l外一点,点A、B、C为直线l上的三点,PA=4,PB=5,PC=2,则点P到直线l的距离为( )
| A. | 2 | B. | 4 | C. | 不大于2 | D. | 小于2 |
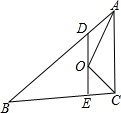 如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长.
如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长.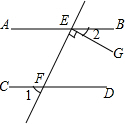 如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.
如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.