题目内容
8.在实数:3.14159,$\root{3}{64}$,1.010010001…,4.21,π,$\frac{22}{7}$,3$\sqrt{2}$中,无理数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.
解答 解:因为3.14159,4.21都是有限小数,
所以它们都是有理数;
因为$\root{3}{64}$=4,4是有限小数,
所以$\root{3}{64}$是有理数;
因为$\frac{22}{7}=3.\stackrel{•}{1}4285\stackrel{•}{7}$,3.$\stackrel{•}{1}4285\stackrel{•}{7}$是无限循环小数,
所以$\frac{22}{7}$是有理数;
因为1.010010001…,π=3.14159265…,3$\sqrt{2}=4.242…$,
所以1.010010001…,π,3$\sqrt{2}$都是无理数.
综上,可得无理数有3个:1.010010001…,π,3$\sqrt{2}$.
点评 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
16.点P为直线l外一点,点A、B、C为直线l上的三点,PA=4,PB=5,PC=2,则点P到直线l的距离为( )
| A. | 2 | B. | 4 | C. | 不大于2 | D. | 小于2 |
13.下面的等式总能成立的是( )
| A. | $\sqrt{{a}^{2}}$=a | B. | $\sqrt{{a}^{2}}$=a2 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{ab}$=$\sqrt{a}$$•\sqrt{b}$ |
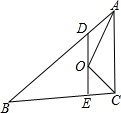 如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长.
如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长. 如图所示,数轴的正半轴上有A、B、C三点,表示1和$\sqrt{2}$的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.
如图所示,数轴的正半轴上有A、B、C三点,表示1和$\sqrt{2}$的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.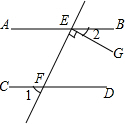 如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.
如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.