题目内容
4. 如图,∠A=2∠ABC,BD平分∠ABC,且AD∥BC,请运用所学知识,求∠ADB的度数.
如图,∠A=2∠ABC,BD平分∠ABC,且AD∥BC,请运用所学知识,求∠ADB的度数.
分析 根据平行线的性质得到∠A+∠ABC=180°,求得∠ABC=60°,由BD平分∠ABC,得出∠ABD,再根据三角形内角和定理即可求出∠ADB.
解答 解:∵AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=2∠ABC,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=$\frac{1}{2}$∠ABC=30°,
又∵∠A=120°,
∴∠ADB=180°-120°-30°=30°.
点评 本题考查了平行线的性质,等腰三角形的判定和性质,角平分线的定义,三角形内角和定理;弄清各个角之间的关系是解决问题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
14. 如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )
如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )
 如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )
如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )| A. | 100° | B. | 130° | C. | 140° | D. | 150° |
12.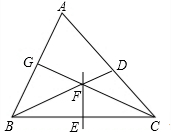 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
19. 如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
 如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
 如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )| A. | $\sqrt{34}$ | B. | 3 | C. | 4 | D. | 5 |
13.下列判断:
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |