题目内容
4.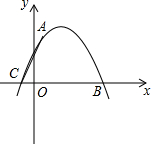 如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).
如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).(1)求该二次函数的解析式;
(2)点D是该二次函数图象上A,B两点之间的一动点,横坐标为x(1<x<5),写出四边形ABCD的面积S关于点D的横坐标x的函数表达式,并求S的最大值;
(3)点E是该二次函数图象上的点,点E是x轴上的点,如果以A、C、E、F为顶点的四边形是以AC为一边的平行四边形,直接写出E的坐标.
分析 (1)把A、B、C的坐标代入二次函数解析式求出a、b、c的值即可;
(2)如图,过A作x轴的垂直,垂足为E(1,0),连接ED、DB,过D作DF⊥AE,DG⊥x轴,垂足分别为F,G,分别表示出三角形ACE,三角形ADE,以及三角形BDE的面积,之和即为S,确定出S关于x的函数解析式,并求出x的范围,利用二次函数性质即可确定出S的最大值,以及此时x的值;
(3)由于AC确定,得到点E与点A的纵坐标之间的关系,然后代入抛物线的解析式,就可得到满足条件的所有点E的坐标.
解答 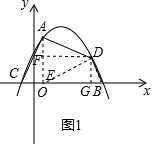 解:(1)把点A(1,4)与B(5,0),C(-1,0)代入y=ax2+bx+c得:$\left\{\begin{array}{l}{a+b+c=4}\\{25a+5b+c=0}\\{a-b+c=0}\end{array}\right.$,
解:(1)把点A(1,4)与B(5,0),C(-1,0)代入y=ax2+bx+c得:$\left\{\begin{array}{l}{a+b+c=4}\\{25a+5b+c=0}\\{a-b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\\{c=\frac{5}{2}}\end{array}\right.$,
∴该二次函数的解析式为:y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$;
(2)如图1,过A作x轴的垂直,垂足为E(1,0),连接ED、DB,过D作DF⊥AE,DG⊥x轴,垂足分别为F,G,
S△ACE=$\frac{1}{2}$CE•AE=$\frac{1}{2}$×2×4=4;
S△ADE=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×4×(x-1)=2x-2;
S△BDE=$\frac{1}{2}$BE•DG=$\frac{1}{2}$×4×(-$\frac{1}{2}$x2+2x+$\frac{5}{2}$)=-x2+4x+5,
则S=S△ACE+S△ADE+S△BDE=4+2x-2-x2+4x+5=-x2+6x+7,
∴S关于x的函数表达式为S=-x2+6x+7(1<x<5),
∵S=-x2+6x+7=-(x-3)2+16,
∴当x=3时,四边形OACB的面积S有最大值,最大值为16;
(3)∵AC为平行四边形的一边,则AC∥EF,AE∥CF,A,E到x轴的距离相等,
∴|yE|=|yA|=4,
∴yE=±4.
当yE=4时,解方程-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=4得,
x1=1,x2=3,
∴点E的坐标为(3,4);
当yE=-4时,解方程-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=-4得,
x1=2-$\sqrt{17}$,x2=2+$\sqrt{17}$,
∴点E的坐标为(2-$\sqrt{17}$,-4),(2+$\sqrt{17}$,-4).
点评 本题属于二次函数综合题,主要考查了运用待定系数法求出直线及抛物线的解析式、抛物线上点的坐标特征、解一元二次方程、平行四边形的性质、抛物线的性质等知识的综合应用,运用割补法及配方法是解决问题的关键,解题时注意运用分类讨论的思想.

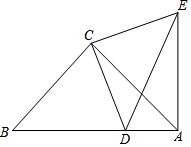 如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点.
如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点.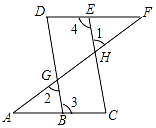 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F