题目内容
3.已知关于x的二次函数y=x2-2ax+3,当1≤x≤3时,函数有最小值2a,则a的值为( )| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
分析 先用配方法把函数化为顶点式的形式,求出其对称轴,再根据二次函数的增减性及题目条件将顶点的横坐标的值分三种情况讨论,从而求出实数a的值.
解答 解:y=x2-2ax+3=(x-a)2+3-a2,
当a≤1时,函数最小,则x=1,1-2a+3=4-2a=2a,
解得:a=1,
∵当1<a<3时,∴x=a时,函数有最小值为:2a,
即3-a2=2a,
解得:a1=-3(不合题意舍去),a2=1,
∴a=1;
当a≥3时,x=3时,9-6a+3=2a,
解得:a=$\frac{3}{2}$(不合题意舍去).
故选:A.
点评 本题考查了求二次函数的最大(小)值的方法.注意,只有当自变量x在整个取值范围内,函数值y才在顶点处取最值.而当自变量取值范围只有一部分时,必须结合二次函数的增减性及对称轴判断何处取最大值,何处取最小值.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.已知关于x的一元二次方程2x2-3kx+4的一个根是1,则k等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | 1 |
18.点A、C为半径是3的圆周上两点,点B为$\widehat{AC}$的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
| A. | $\sqrt{5}$或2$\sqrt{2}$ | B. | $\sqrt{5}$或2$\sqrt{3}$ | C. | $\sqrt{6}$或2$\sqrt{2}$ | D. | $\sqrt{6}$或2$\sqrt{3}$ |
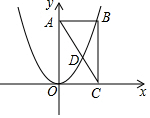 如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$. 如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)
如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)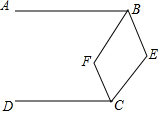 如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.
如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.