题目内容
18.点A、C为半径是3的圆周上两点,点B为$\widehat{AC}$的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )| A. | $\sqrt{5}$或2$\sqrt{2}$ | B. | $\sqrt{5}$或2$\sqrt{3}$ | C. | $\sqrt{6}$或2$\sqrt{2}$ | D. | $\sqrt{6}$或2$\sqrt{3}$ |
分析 过B作直径,连接AC交AO于E,①如图①,根据已知条件得到BD=$\frac{1}{3}$×2×3=2,如图②,BD=$\frac{2}{3}$×2×3=4,求得OD=1,OE=2,DE=1,连接OD,根据勾股定理得到结论,
解答 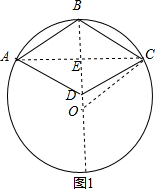 解:过B作直径,连接AC交AO于E,
解:过B作直径,连接AC交AO于E,
∵点B为$\widehat{AC}$的中点,
∴BD⊥AC,
①如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=$\frac{1}{3}$×2×3=2,
∴OD=OB-BD=1,
∵四边形ABCD是菱形,
∴DE=$\frac{1}{2}$BD=1,
∴OE=2,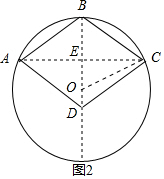
连接OD,
∵CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{5}$,
∴边CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{6}$;
如图②,BD=$\frac{2}{3}$×2×3=4,
同理可得,OD=1,OE=1,DE=2,
连接OD,
∵CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,
∴边CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{(2\sqrt{2})^{2}+{2}^{2}}$=2$\sqrt{3}$,
故选D.
点评 本题考查了圆心角,弧,弦的关系,勾股定理,菱形的性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
3.已知关于x的二次函数y=x2-2ax+3,当1≤x≤3时,函数有最小值2a,则a的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
7.关于抛物线y=x2-(a+1)x+a-2,下列说法错误的是( )
| A. | 开口向上 | B. | 当a=2时,经过坐标原点O | ||
| C. | 不论a为何值,都过定点(1,-2) | D. | a>0时,对称轴在y轴的左侧 |
8.四根长度分别为4cm、6cm、10cm、14cm的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
| A. | 20cm | B. | 24cm | C. | 28cm | D. | 30cm |


 如图,菱形ABCD中,对角线AC交BD于O,E是CD的中点,且OE=2,则菱形ABCD的周长等于16.
如图,菱形ABCD中,对角线AC交BD于O,E是CD的中点,且OE=2,则菱形ABCD的周长等于16.