题目内容
17.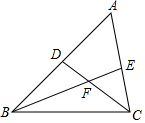 如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )| A. | 100° | B. | 115° | C. | 130° | D. | 135° |
分析 根据三角形内角和定理求出∠ABC+∠ACB,根据内心的概念得到FB、FC分别是∠ABC、∠ACB的平分线,根据三角形内角和定理、角平分线的定义计算即可.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵点F是△ABC的内心,
∴FB、FC分别是∠ABC、∠ACB的平分线,
∴∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠BFC=180°-(∠FBC+∠FCB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=115°,
故选:B.
点评 本题考查的是三角形的内切圆和内心,掌握三角形内角和定理、内心的概念和性质是解题的关键.

练习册系列答案
相关题目
7. 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
8.在函数y=$\sqrt{x-2}$中,自变量x的取值范围是( )
| A. | x<2 | B. | x≤2 | C. | x>2 | D. | x≥2 |
5.一元二次方程x2+2x+2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
12. 小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )
小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )
 小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )
小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )| A. | 城 | B. | 明 | C. | 全 | D. | 国 |
9.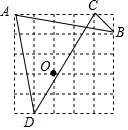 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的内心 |
 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.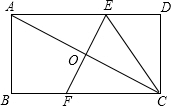 如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$.
如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$. 如图,CD是△ABC的中线,CE是△ABC的高,若AC=9,BC=12,AB=15.
如图,CD是△ABC的中线,CE是△ABC的高,若AC=9,BC=12,AB=15.