题目内容
2. 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
分析 设AB=x,由矩形的性质和旋转的性质可知AB=C'D=x,A'C=A'D+CD=x+2,由已知条件易证△AC'D∽△ABC,由相似三角形的性质可求出x的值,在直角三角形ABC'中即可求出tan∠ABA′的值.
解答 解:
∵四边形ABCD是矩形,
∴AD=BC=2,∠A=90°,C'D∥BC,
∵将矩形ABCD绕点D顺时针旋转90°,
∴AB=C'D,BC=B'C'=AD=2,
设AB=x,则AB=C'D=x,A'C=A'D+CD=x+2,
∵C'D∥BC,
∴△AC'D∽△ABC,
∴C'D:BC=AD:DC,
即x:2=2:x+2,
解得:x=-1+$\sqrt{5}$或x=-1-$\sqrt{5}$(小于0,不合题意,舍去),
∴AC'=2-C'D=2-(-1+$\sqrt{5}$)=3-$\sqrt{5}$
∴tan∠ABA′=$\frac{AC′}{AB}$=$\frac{3-\sqrt{5}}{-1+\sqrt{5}}$=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题主要考查矩形的性质、旋转的性质及三角函数的定义,利用旋转的性质和相似三角形的性质求得矩形的宽是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
12.若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式是( )
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
17.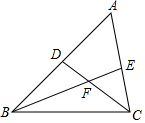 如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
 如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )| A. | 100° | B. | 115° | C. | 130° | D. | 135° |
7.如图,DE∥AB,则∠B的大小为( )

| A. | 42° | B. | 45° | C. | 48° | D. | 58° |
12.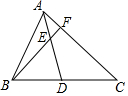 如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )
如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )
 如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )
如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )



 如图,二次函数y=a(x-2)2+k的图象与x轴交于A,B两点,且点A的横坐标为-1,则点B的横坐标为5.
如图,二次函数y=a(x-2)2+k的图象与x轴交于A,B两点,且点A的横坐标为-1,则点B的横坐标为5.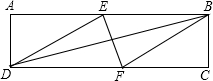 在矩形ABCD中有一个菱形BEDF(点E、F分别在线段AB、CD上)记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,给出如下结论:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正确的结论的序号是①③④(把所有正确结论的序号都填在横线上)
在矩形ABCD中有一个菱形BEDF(点E、F分别在线段AB、CD上)记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,给出如下结论:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正确的结论的序号是①③④(把所有正确结论的序号都填在横线上)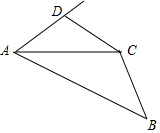 如图,AC平分∠DAB,∠ADC+∠B=180°,求证:CD=CB.
如图,AC平分∠DAB,∠ADC+∠B=180°,求证:CD=CB.