题目内容
6.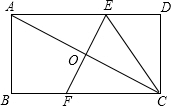 如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$.
如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$.
分析 由四边形ABCD是矩形,得到CD=AB=2,AD=BC=3,∠D=90°,根据折叠的性质得到AE=CE,根据勾股定理列方程即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠D=90°,
∵将矩形纸片ABCD折叠,使得点A和点C重合,
∴AE=CE,
∴DE=AD-AE=3-CE,
∵CE2=DE2+CD2,
即CE2=(3-CE)2+22,
∴CE=$\frac{13}{6}$.
点评 本题主要考查的是翻折的性质,矩形的性质、勾股定理的应用,利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.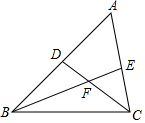 如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
 如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )
如图,点F是△ABC的内心,∠A=50°,则∠BFC=( )| A. | 100° | B. | 115° | C. | 130° | D. | 135° |
1.下列关于矩形的说法,正确的是( )
| A. | 对角线相等的四边形是矩形 | B. | 对角线互相平分的四边形是矩形 | ||
| C. | 矩形的对角线相等且互相平分 | D. | 矩形的对角线互相垂直且平分 |
18.下列三条线段不能构成三角形的三边的是( )
| A. | 3cm,4cm,5cm | B. | 5cm,6cm,11cm | C. | 5cm,6cm,10cm | D. | 2cm,3cm,4cm |
15.下列说法中,正确的是( )
| A. | 有一个角是直角的四边形是菱形 | |
| B. | 对角线互相垂直的菱形是正方形 | |
| C. | 对角线相等的平行四边形是矩形 | |
| D. | 一组邻边相等的平行四边形是正方形 |




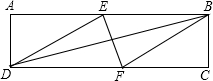 在矩形ABCD中有一个菱形BEDF(点E、F分别在线段AB、CD上)记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,给出如下结论:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正确的结论的序号是①③④(把所有正确结论的序号都填在横线上)
在矩形ABCD中有一个菱形BEDF(点E、F分别在线段AB、CD上)记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,给出如下结论:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正确的结论的序号是①③④(把所有正确结论的序号都填在横线上)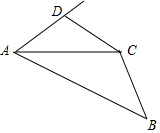 如图,AC平分∠DAB,∠ADC+∠B=180°,求证:CD=CB.
如图,AC平分∠DAB,∠ADC+∠B=180°,求证:CD=CB.