题目内容
4.若关于x的方程x2-2(1-k)x+k2=0有实数根m和n,则m+n的取值范围是( )| A. | m+n≥1 | B. | m+n≤1 | C. | m+n≥$\frac{1}{2}$ | D. | m+n≤$\frac{1}{2}$ |
分析 根据方程有实数根,求出k的取值范围,再根据根与系数的关系求出m+n的取值范围.
解答 解:∵关于x的方程x2-2(1-k)x+k2=0有实数根m,n,
∴△=[-2(1-k)]2-4×1×k2≥0,
解得k≤$\frac{1}{2}$,
∵m,n是一元二次方程的两个根,
∴m+n=2(1-k)=2-2k,
又∵k≤$\frac{1}{2}$,
∴α+β≥1.
故选:A.
点评 此题主要考查了根与系数的关系,将根与系数的关系与不等式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
17. 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m=10;n=50
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.01 |
| B | m | n | 0.01 |
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m=10;n=50
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
14.如果一个角等于25°,那么它的余角是( )
| A. | 25° | B. | 65° | C. | 155° | D. | 75° |
 如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.
如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.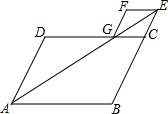 如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.
如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形. 如图,在线段AC、BC、CD中,线段CD最短,理由是垂线段最短.
如图,在线段AC、BC、CD中,线段CD最短,理由是垂线段最短.