题目内容
2. 如图,已知在正方形ABCD中,AE=EB,AF=$\frac{1}{4}$AD,求证:CE⊥EF.
如图,已知在正方形ABCD中,AE=EB,AF=$\frac{1}{4}$AD,求证:CE⊥EF.
分析 连接CF,根据已知条件,运用勾股定理可以分别求出△CEF的三边,根据勾股定理的逆定理即可求解.
解答  证明:连接CF,设正方形的边长为4,
证明:连接CF,设正方形的边长为4,
∵四边形ABCD为正方形,
∴设AB=BC=CD=DA=4,
∵点E为AB中点,AF=$\frac{1}{4}$AD,
∴AE=BE=2,AF=1,DF=3,
由勾股定理得:
EF2=12+22=5,EC2=22+42=20,FC2=42+32=25.
∵EF2+EC2=FC2,
∴△CFE是直角三角形,
∴∠FEC=90°,即EF⊥CE.
点评 本题综合运用勾股定理及其逆定理,此题难度一般,解答本题的关键是掌握勾股定理.

练习册系列答案
相关题目
10. 如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )
如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )
 如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )
如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )| A. | 105° | B. | 112.5° | C. | 135° | D. | 157.5° |
17.下列运算中错误的是( )
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{8}÷\sqrt{2}=2$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | ${(-\sqrt{3})^2}=3$ |
14.如果一个角等于25°,那么它的余角是( )
| A. | 25° | B. | 65° | C. | 155° | D. | 75° |
 如图,在线段AC、BC、CD中,线段CD最短,理由是垂线段最短.
如图,在线段AC、BC、CD中,线段CD最短,理由是垂线段最短.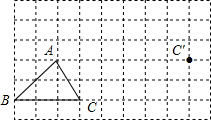 如图,△ABC平移后的图形是△A′B′C′,其中C和C′是对应点,请画出平移后的三角形A′B′C′.
如图,△ABC平移后的图形是△A′B′C′,其中C和C′是对应点,请画出平移后的三角形A′B′C′.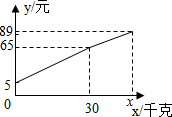 一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:
一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题: