题目内容
15.从-1,0,$\frac{1}{3}$,π,$\sqrt{3}$中随机任取一数,取到无理数的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由题意可得共有5种等可能的结果,其中无理数有π,$\sqrt{3}$共2种情况,则可利用概率公式求解.
解答 解:∵共有5种等可能的结果,无理数有:π,$\sqrt{3}$共2种情况,
∴取到无理数的概率是:$\frac{2}{5}$.
故选B.
点评 此题考查了概率公式的应用与无理数的定义.此题比较简单,注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.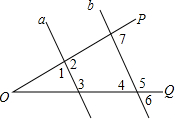 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )| A. | ∠3+∠4=180° | B. | ∠2+∠5>180° | C. | ∠1+∠6<180° | D. | ∠2+∠7=180° |
3.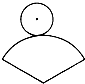 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )| A. | 2$\sqrt{2}$r | B. | r | C. | $\sqrt{10}$r | D. | 3r |
7.若把函数y=(x-3)2-2的图象向左平移a个单位,再向上平移b(b>0)个单位,所得图象的函数表达式是y=(x+3)2+2,则( )
| A. | a=6,b=4 | B. | a=-6,b=4 | C. | a=6,b=-4 | D. | a=-6,b=-4 |
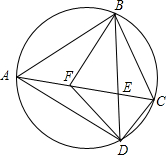 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.
如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.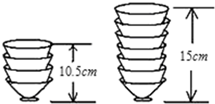 如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:
如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题: 某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.
某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.