题目内容
12.如图,图①、图②、图③分别是直角三角形、锐角三角形、钝角三角形,∠A、∠B、∠C的对边的长度分别为a、b、c.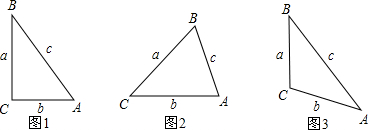
请阅读下列材料:
在图①中,由勾股定理,a、b、c三边的关系是:a2+b2=c2;在图②中,作BD⊥CA于D,如图.设CD=x,在Rt△BCD中,BD2=a2-x2;在Rt△BAD,BD2=c2-(b-x)2,所以a2-x2=c2-(b-x)2,化简得a2+b2=c2+2bx.
因为b>0,x>0,所以2bx>0,所以a、b、c三边的关系是:a2+b2>c2.
根据以上材料,试猜想:在钝角三角形中,a、b、c三边的关系,并证明你的猜想.
分析 作BD⊥CA于D,设CD=x,在Rt△BCD和Rt△BAD中,利用勾股定理得出猜想结论a2+b2<c2即可.
解答 猜想:在钝角三角形中,a、b、c三边的关系为a2+b2<c2.
证明:如图,
作BD⊥CA于D,设CD=x,
在Rt△BCD中,
BD2=a2-x2;
在Rt△BAD,
BD2=c2-(b+x)2,
所以a2-x2=c2-(b+x)2,
化简得a2+2bx+b2=c2,
∵b>0,x>0,
∴2bx>0,
∴a、b、c三边的关系是:a2+b2<c2.
点评 此题考查勾股定理的运用,构造直角三角形,利用勾股定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.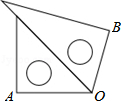 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )
 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )| A. | 60° | B. | 75° | C. | 105° | D. | 180° |
3.已知a<b,下面四个不等式中不正确的是( )
| A. | 3a<3b | B. | a+3<b+3 | C. | -3a<-3b | D. | a-3<b-3 |
20.下列方程没有实数根的是( )
| A. | x2+3x+4=0 | B. | (x-2)2=5 | C. | 2x2+7x-1=0 | D. | x2+5x+3=0 |
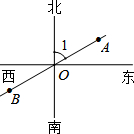 如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.
如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.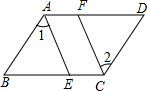 如图,在四边形ABCD中,已知AD∥BC,∠DAB=∠BCD,∠1=∠2,在说明AE∥CF的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AD∥BC,∠DAB=∠BCD,∠1=∠2,在说明AE∥CF的解答过程中,填上适当的理由.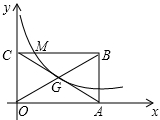 如图,矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上,点G为矩形对角线的交点,经过点G的双曲线y=$\frac{k}{x}$在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为8.
如图,矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上,点G为矩形对角线的交点,经过点G的双曲线y=$\frac{k}{x}$在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为8.