题目内容
4.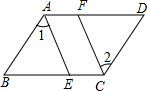 如图,在四边形ABCD中,已知AD∥BC,∠DAB=∠BCD,∠1=∠2,在说明AE∥CF的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AD∥BC,∠DAB=∠BCD,∠1=∠2,在说明AE∥CF的解答过程中,填上适当的理由.解:∵∠DAB=∠BCD,∠1=∠2(已知)
∴∠DAE=∠BCF(等式的性质)
∵AD∥BC(已知)
∴∠BCF=∠DFC两直线平行,内错角相等
∴∠DAE=∠DFC等量代换
∴AE∥CF同位角相等,两直线平行.
分析 先根据∠DAB=∠BCD,∠1=∠2得出∠DAE=∠BCF,再由AD∥BC得出∠BCF=∠DFC,故可得出∠DAE=∠DFC,由此可得出结论.
解答 解:∵∠DAB=∠BCD,∠1=∠2(已知)
∴∠DAE=∠BCF(等式的性质).
∵AD∥BC(已知),
∴∠BCF=∠DFC(两直线平行,内错角相等),
∴∠DAE=∠DFC(等量代换),
∴AE∥CF(同位角相等,两直线平行).
故答案为:两直线平行,内错角相等,等量代换,同位角相等,两直线平行.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
16. 一物体及主视方向如图所示,则它的俯视图是( )
一物体及主视方向如图所示,则它的俯视图是( )
 一物体及主视方向如图所示,则它的俯视图是( )
一物体及主视方向如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
14.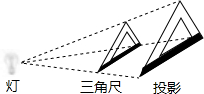 如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,若三角尺的一边长为8cm,则这条边在投影中的对应边长为( )
如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,若三角尺的一边长为8cm,则这条边在投影中的对应边长为( )
 如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,若三角尺的一边长为8cm,则这条边在投影中的对应边长为( )
如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,若三角尺的一边长为8cm,则这条边在投影中的对应边长为( )| A. | 8cm | B. | 12cm | C. | 16cm | D. | 24cm |
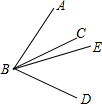 如图,∠ABC=30°,∠CBD=50°,BE平分∠ABD,则∠CBE=10°.
如图,∠ABC=30°,∠CBD=50°,BE平分∠ABD,则∠CBE=10°.
 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求从C看A、B的视角?
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求从C看A、B的视角?