Question

1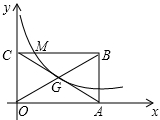．如图，矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上，点G为矩形对角线的交点，经过点G的双曲线y=$\frac{k}{x}$在第一象限的图象与BC相交于点M，交AB于N，若已知S_△MBN=9，则k的值为8．

Answer 1

分析 设出点G的坐标，由矩形的性质得到点B的坐标，根据点G，M，N都在双曲线上，由G得坐标求出M，N的坐标，根据三角形的面积公式列方程求出ab的值即k的值．

解答 解设点G的坐标（a，b），则B（2a，2b），
∴ab=k，
∵M点在矩形的边BC上，
∴点M的纵坐标=2b，
∵点M在双曲线y=$\frac{k}{x}$上，
∴M（$\frac{a}{2}$，2b），同理N（2a，$\frac{b}{2}$），
∴BM=2a-$\frac{a}{2}$，BN=2b-$\frac{b}{2}$，
∵S_△MBN=9，
∴$\frac{1}{2}$BM•BN=$\frac{1}{2}$（2a-$\frac{a}{2}$）（2b-$\frac{b}{2}$）=$\frac{9ab}{8}$=9，
∴ab=k=8，
∴k=8．

点评 本题主要考查反比例函数系数k的几何意义，矩形的性质，点的坐标的求法，关键是设出点G的坐标．