题目内容
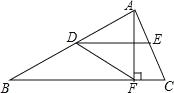
如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4 B.8 C.2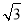 D.4
D.4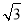
 D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D.
D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D.
 阅读快车系列答案
阅读快车系列答案不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A.  B.
B. 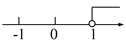 C.
C. 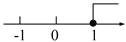 D.
D. 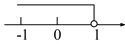
 D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D.
D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D. 若a>c,则当m_________时,am<cm; 当m_________时,am=cm.
 <0 =0
【解析】根据不等式的基本性质:不等式两边乘(或除以)同一个负数,不等号的方向改变,可知m<0.
∵a>c,
又知:am<cm,
∴根据不等式的基本性质3可得:
m<0;
又知:am=cm,
∴m=0.
故答案为:<0;=0.
<0 =0
【解析】根据不等式的基本性质:不等式两边乘(或除以)同一个负数,不等号的方向改变,可知m<0.
∵a>c,
又知:am<cm,
∴根据不等式的基本性质3可得:
m<0;
又知:am=cm,
∴m=0.
故答案为:<0;=0. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2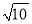 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
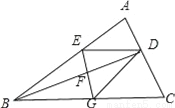
 (1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:...
(1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:... 如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
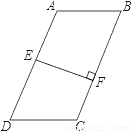
 (1)15;(2)=.
【解析】试题分析:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
(2)如图,连接EC,延长CD、BE交于点P,
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵,
∴△ABE≌△D...
(1)15;(2)=.
【解析】试题分析:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
(2)如图,连接EC,延长CD、BE交于点P,
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵,
∴△ABE≌△D... 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
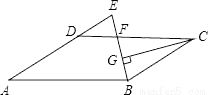
A. 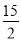 B.
B. 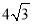 C.
C. 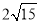 D.
D. 
 C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2...
C
【解析】∵∠ABC的平分线交CD于点F,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,
∴DE=4,
∵DC∥AB,
∴,
∴,
∴EB=6,
∵CF=CB,CG⊥BF,
∴BG=BF=2... 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=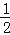 BC,连接CD和EF.
BC,连接CD和EF.
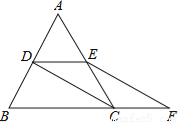
(1)求证:DE=CF;
(2)求EF的长.
 见解析;
【解析】试题分析:(1)直接利用三角形中位线定理得出DEBC,进而得出DE=FC;
(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长
试题解析:(1)证明:∵D、E分别为AB、AC的中点, ∴DEBC,
∵延长BC至点F,使CF=BC, ∴DEFC, 即DE=CF;
(2)【解析】
∵DEFC, ∴四边形DE...
见解析;
【解析】试题分析:(1)直接利用三角形中位线定理得出DEBC,进而得出DE=FC;
(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长
试题解析:(1)证明:∵D、E分别为AB、AC的中点, ∴DEBC,
∵延长BC至点F,使CF=BC, ∴DEFC, 即DE=CF;
(2)【解析】
∵DEFC, ∴四边形DE... 如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
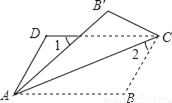
A. 66° B. 104° C. 114° D. 124°
 C
【解析】试题解析:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°;
故选C.
C
【解析】试题解析:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°;
故选C. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)记抛物线顶点为D,求△BCD的面积;
(2)若直线y=﹣ x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
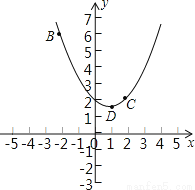
 (1)3 (2)<b≤3.
【解析】(1)根据待定系数法即可解决问题.求出直线BC与对称轴的交点H,根据S△BDC=S△BDH+S△DHC即可解决问题.
(2)由,当方程组只有一组解时求出b的值,当直线y=﹣x+b经过点C时,求出b的值,当直线y=﹣x+b经过点B时,求出b的值,由此即可解决问题.
【解析】
(1)由题意解得,
∴抛物线解析式为y=x2﹣x+2.
∵...
(1)3 (2)<b≤3.
【解析】(1)根据待定系数法即可解决问题.求出直线BC与对称轴的交点H,根据S△BDC=S△BDH+S△DHC即可解决问题.
(2)由,当方程组只有一组解时求出b的值,当直线y=﹣x+b经过点C时,求出b的值,当直线y=﹣x+b经过点B时,求出b的值,由此即可解决问题.
【解析】
(1)由题意解得,
∴抛物线解析式为y=x2﹣x+2.
∵... 
