题目内容
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)记抛物线顶点为D,求△BCD的面积;
(2)若直线y=﹣ x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
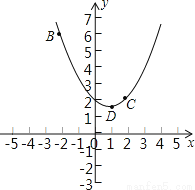
 (1)3 (2)<b≤3.
【解析】(1)根据待定系数法即可解决问题.求出直线BC与对称轴的交点H,根据S△BDC=S△BDH+S△DHC即可解决问题.
(2)由,当方程组只有一组解时求出b的值,当直线y=﹣x+b经过点C时,求出b的值,当直线y=﹣x+b经过点B时,求出b的值,由此即可解决问题.
【解析】
(1)由题意解得,
∴抛物线解析式为y=x2﹣x+2.
∵...
(1)3 (2)<b≤3.
【解析】(1)根据待定系数法即可解决问题.求出直线BC与对称轴的交点H,根据S△BDC=S△BDH+S△DHC即可解决问题.
(2)由,当方程组只有一组解时求出b的值,当直线y=﹣x+b经过点C时,求出b的值,当直线y=﹣x+b经过点B时,求出b的值,由此即可解决问题.
【解析】
(1)由题意解得,
∴抛物线解析式为y=x2﹣x+2.
∵...
 名校课堂系列答案
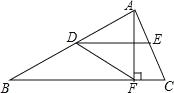
名校课堂系列答案如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4 B.8 C.2 D.4
D.4
 D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D.
D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为点F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

 (1)证明见解析(2)证明见解析
【解析】证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF =∠AEB= 30º,AE=AB,∠EFA= 90º.
∵∠ACB= 90º,∠BAC= 30º,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△AEF≌△BAC.
∴AC = EF.
(2)∵△ACD是等边三角形,
∴AC = AD,∠DAC=...
(1)证明见解析(2)证明见解析
【解析】证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF =∠AEB= 30º,AE=AB,∠EFA= 90º.
∵∠ACB= 90º,∠BAC= 30º,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△AEF≌△BAC.
∴AC = EF.
(2)∵△ACD是等边三角形,
∴AC = AD,∠DAC=... 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A. 7 B. 10 C. 35 D. 70
 C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C.
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C. 自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
【解析】
设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣2x﹣3>0.
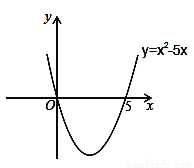
 (1)①,③(2)0<x<5(3)x<﹣1,或x>3.
【解析】试题分析:(1)解题过程中,渗透了转化思想和数形结合思想;
(2)观察图象即可写出一元二次不等式:x2﹣5x<0的解集;
(3)先设函数解析式,根据a的值确定抛物线的开口向上,再找出抛物线与x轴相交的两点,就可以画出抛物线,根据y>0确定一元二次不等式x2﹣2x﹣3>0的解集.
试题解析:【解析】
(1)上述...
(1)①,③(2)0<x<5(3)x<﹣1,或x>3.
【解析】试题分析:(1)解题过程中,渗透了转化思想和数形结合思想;
(2)观察图象即可写出一元二次不等式:x2﹣5x<0的解集;
(3)先设函数解析式,根据a的值确定抛物线的开口向上,再找出抛物线与x轴相交的两点,就可以画出抛物线,根据y>0确定一元二次不等式x2﹣2x﹣3>0的解集.
试题解析:【解析】
(1)上述... 如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为 .
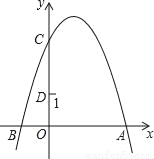
 (1+,2)或(1﹣,2).
【解析】【解析】
∵△PCD是以CD为底的等腰三角形,∴点P在线段CD的垂直平分线上,如图,过P作PE⊥y轴于点E,则E为线段CD的中点,∵抛物线与y轴交于点C,∴C(0,3),且D(0,1),∴E点坐标为(0,2),∴P点纵坐标为2,在中,令y=2,可得,解得x=,∴P点坐标为(,2)或(,2),故答案为:(,2)或(,2).
(1+,2)或(1﹣,2).
【解析】【解析】
∵△PCD是以CD为底的等腰三角形,∴点P在线段CD的垂直平分线上,如图,过P作PE⊥y轴于点E,则E为线段CD的中点,∵抛物线与y轴交于点C,∴C(0,3),且D(0,1),∴E点坐标为(0,2),∴P点纵坐标为2,在中,令y=2,可得,解得x=,∴P点坐标为(,2)或(,2),故答案为:(,2)或(,2). 将抛物线y=ax2﹣1平移后与抛物线y=a(x﹣1)2重合,抛物线y=ax2﹣1上的点A(2,3)同时平移到A′,那么点A′的坐标为( )
A. (3,4) B. (1,2) C. (3,2) D. (1,4)
 A
【解析】【解析】
∵抛物线y=ax2﹣1的顶点坐标是(0,﹣1),抛物线y=a(x﹣1)2的顶点坐标是(1,0),∴将抛物线y=ax2﹣1向右平移1个单位,再向上平移1个单位得到抛物线y=a(x﹣1)2,∴将点A(2,3)向右平移1个单位,再向上平移1个单位得到点A′的坐标为(3,4).
故选A.
A
【解析】【解析】
∵抛物线y=ax2﹣1的顶点坐标是(0,﹣1),抛物线y=a(x﹣1)2的顶点坐标是(1,0),∴将抛物线y=ax2﹣1向右平移1个单位,再向上平移1个单位得到抛物线y=a(x﹣1)2,∴将点A(2,3)向右平移1个单位,再向上平移1个单位得到点A′的坐标为(3,4).
故选A. 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
 B
【解析】试题分析:关于x的一元二次方程x2-3x+m=0的两实数根就是二次函数y=x2-3x+m(m为常数)的图象与x轴的两个交点的横坐标.∵二次函数的解析式是y=x2-3x+m(m为常数),∴该抛物线的对称轴是:x=.
又∵二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),
∴根据抛物线的对称性质知,该抛物线与x轴的另一个交点的坐标是(2,0),
...
B
【解析】试题分析:关于x的一元二次方程x2-3x+m=0的两实数根就是二次函数y=x2-3x+m(m为常数)的图象与x轴的两个交点的横坐标.∵二次函数的解析式是y=x2-3x+m(m为常数),∴该抛物线的对称轴是:x=.
又∵二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),
∴根据抛物线的对称性质知,该抛物线与x轴的另一个交点的坐标是(2,0),
... 在边长为1个单位长度的小正方形组成的网格中,点A、B、C、O都是格点.
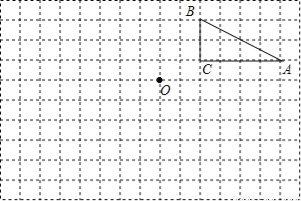
(1)将△ABC向左平移6个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2.
 (1)作图见解析;(2)作图见解析.
【解析】试题分析:(1)把A、B、C三点分别向左平移6个单位长度,即可得到三个顶点的对应点,然后顺次连接三点即可;
(2)连接AO并延长,然后截取OA2=OA,则A2就是A的对应点,同样可以作出B、C的对应点,然后顺次连接即可.
【解析】
(1)所作图形如图所示;
(2)所作图形如图所示.
(1)作图见解析;(2)作图见解析.
【解析】试题分析:(1)把A、B、C三点分别向左平移6个单位长度,即可得到三个顶点的对应点,然后顺次连接三点即可;
(2)连接AO并延长,然后截取OA2=OA,则A2就是A的对应点,同样可以作出B、C的对应点,然后顺次连接即可.
【解析】
(1)所作图形如图所示;
(2)所作图形如图所示. 
