题目内容
8.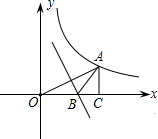 如图,点A(3,m)在双曲线y=$\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABO的面积为( )
如图,点A(3,m)在双曲线y=$\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABO的面积为( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 先根据反比例函数图象上点的坐标特征求出m=1,得到OC=3,AC=1,再利用线段垂直平分线的性质得到AB=OB,然后把△ABC的周长化为OC+AC求解.
解答 解:∵点A(3,m)在双曲线y=$\frac{3}{x}$上,
∴3m=3,解得m=1,
即A(3,1),
∴OC=3,AC=1,
∵线段OA的垂直平分线交OC于点B,
∴AB=OB,
∴AB2=(OC-OB)2+AC2,
∴AB2=(3-AB)2+12,
∴AB=OB=$\frac{5}{3}$,
∴S△ABO=$\frac{1}{2}$BO•AC=$\frac{5}{6}$,
故选A.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了线段垂直平分线的性质.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
16.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
17.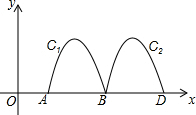 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )| A. | -2<m<$\frac{1}{8}$ | B. | -3<m<-$\frac{7}{4}$ | C. | -3<m<-2 | D. | -3<m<-$\frac{15}{8}$ |
18.把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )
| A. |  | B. |  | C. |  | D. |  |
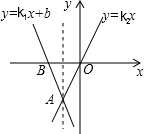 如图,直线y=k1x+b经过点A(-1,-2)和点B(-2,0),直线y=k2x经过点A,则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,不等式k2x<k1x+b<0的解集为x<-1.
如图,直线y=k1x+b经过点A(-1,-2)和点B(-2,0),直线y=k2x经过点A,则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,不等式k2x<k1x+b<0的解集为x<-1.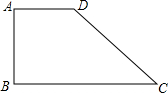 如图,直角梯形ABCD是一机器零件的横断面,已知DC=20cm,BC=40cm,∠DCB=30°,求AD的长为40-10$\sqrt{3}$cm.
如图,直角梯形ABCD是一机器零件的横断面,已知DC=20cm,BC=40cm,∠DCB=30°,求AD的长为40-10$\sqrt{3}$cm.