题目内容
16.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
分析 首先根据一次函数y2=dx+e(d≠0)的图象经过点(x1,0),可得y2=d(x-x1),y=y1+y2=ax2+(d-ax2-ax1)x+ax1x2-dx1;然后根据函数y=y1+y2的图象与x轴仅有一个交点,可得函数y=y1+y2与x轴的交点为(x1,0),再结合对称轴公式求解.
解答 解:∵一次函数y2=dx+e(d≠0)的图象经过点(x1,0),
∴dx1+e=0,
∴y2=d(x-x1),
∴y=y1+y2=a(x-x1)(x-x2)+d(x-x1)
=ax2-axx2-ax1x+ax1x2+dx-dx1
=ax2+(d-ax2-ax1)x+ax1x2-dx1
∵当x=x1时,y1=0,y2=0,
∴当x=x1时,y=y1+y2=0,
∵y=ax2+(d-ax2-ax1)x+ax1x2-dx1与x轴仅有一个交点,
∴y=y1+y2的图象与x轴的交点为(x1,0)
∴$-\frac{d-a{x}_{2}-a{x}_{1}}{2a}$=x1,
化简得:a(x2-x1)=d
故选:B.
点评 此题主要考查了抛物线与x轴的交点问题,以及曲线上点的坐标与方程的关系,要熟练掌握,解答此题的关键是判断出:函数y=y1+y2与x轴的交点为(x1,0).

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
11.两个正数满足a-b=2,ab=t-1,设p=(a+b)2,则P关于t的函数图象是( )
| A. | 射线(不含端点) | B. | 线段(不含端点) | C. | 直线 | D. | 抛物线的一部分 |
8.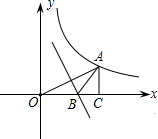 如图,点A(3,m)在双曲线y=$\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABO的面积为( )
如图,点A(3,m)在双曲线y=$\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABO的面积为( )
 如图,点A(3,m)在双曲线y=$\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABO的面积为( )
如图,点A(3,m)在双曲线y=$\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABO的面积为( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
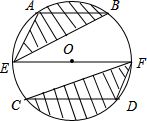 如图,⊙O的直径EF为10cm,弦AB、CD分别为6cm、8cm,且AB∥EF∥CD.求图中阴影部分面积之和.
如图,⊙O的直径EF为10cm,弦AB、CD分别为6cm、8cm,且AB∥EF∥CD.求图中阴影部分面积之和.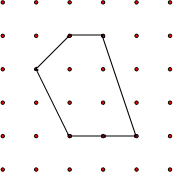 各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6
各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6